Точка и прямая в плоскости

Способы задания плоскости на чертеже

ПРОЕКЦИИ ПЛОСКОСТИ

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис. 29);

 

а) модель	б) эпюр
Рисунок 29. Плоскость, заданная тремя точками, не лежащими на одной прямой

 

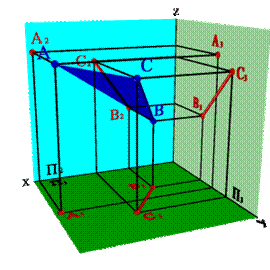
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 30);

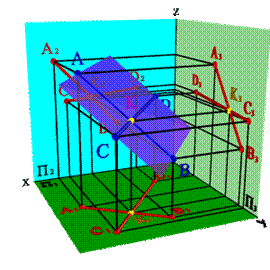
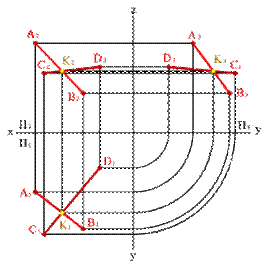
3. двумя пересекающимися прямыми (рис. 31);

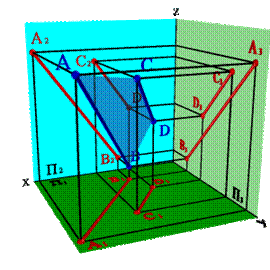
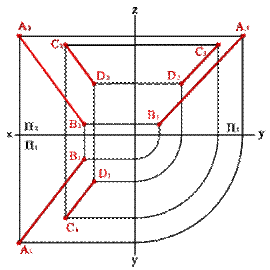
4. двумя параллельными прямыми (рис. 32);

 

 

а) модель	б) эпюр
Рисунок 30. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии
а) модель	б) эпюр
Рисунок 31. Плоскость, заданная двумя пересекающимися прямыми
а) модель	б) эпюр
Рисунок 32. Плоскость, заданная двумя параллельными прямыми

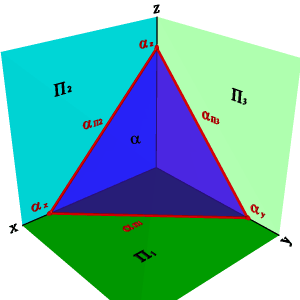
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис. 33).

Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная плоскость различают горизонтальный, фронтальный и профильный следы.

а) модель	б) эпюр
Рисунок 33. Плоскость, заданная следами

 

Следы плоскости общего положения пересекаются попарно на осях в точках a_x,a_y,a_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

 

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.

Если точка принадлежит плоскости, то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.

Рассмотрим пример (рис. 34). Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(ab).

 

а) модель	б) эпюр
Рисунок 34. Точка, принадлежащая плоскости

 

Через точку А₂ проведем проекцию прямой m₂, пересекающую проекции прямых a₂и b₂ в точках С₂ и В₂ (СÎa,BÎaÞ mÎa). Построив проекции точек С₁ и В₁, определяющие положение m₁, находим горизонтальную проекцию точки А (А₁Î m₁, m ÎaÞ АÎa).

Сформулируем теперь условие принадлежности прямой плоскости как аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если она проходит через две точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Проиллюстрируем примерами использование этих аксиом.

Пусть требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k (рис. 35).

Проекция прямой m₂ пересекает проекции прямых n₂ и k₂ в точках В₂ и С₂ соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.

Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.

Пусть теперь через точку В необходимо провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис. 36).

Пусть точка В принадлежит прямой n, лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В₂ проведем проекцию прямой m₂ параллельно прямой k₂, для нахождения недостающих проекций прямой необходимо построить проекцию точки В₁, как точки лежащей на проекции прямой n₁ и через неё провести проекцию прямой m₁ параллельно проекции k₁.

Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме 2 прямая принадлежит этой плоскости.