Атомы и линейные молекулы.

. .

. .

.

. .

Классификация точечных групп.

Произведения групп.

Одной из операций, которые могут быть определены для групп, является произведение независимых групп. Если группа А состоит из n элементов, а B из m элементов, то их произведение содержит n´m элементов вида A_iB_j. Например, произведением групп {Е, C₃и C₃ ² }и {E, s_v}является:

{Е, C₃, C₃ ² }´{E, s_v}= (Е, C₃, C₃ ² , s_v,s_v¢ , s_v² ) [ рассмотреть подробнее]

Т.о. группа C_3v порождена произведением своих двух независимых подгрупп. В то же время подгруппы {E, s_v}и {E, s_v¢ } не порождают группы:

{E, s_v}´{E, s_v¢ }= (Е, s_v, s_v¢ , C₃ ² ).

Если мы умножим {E, s_v}´{Е, C₃, C₃ ² }= (Е, C₃, C₃ ² , s_v, s_v² ,s_v¢ ) то получим те же элементы, что и выше, но в другом порядке. Т.к. C₃и C₃ ² не коммутируют с s_v. Произведения групп с некоммутирующими элементами называют полупрямыми (обозначают символом ^). Произведения с коммутирующими элементами называют прямыми ( символом ´). Таким образом, если обозначим группу {E, s_v}как C_s, то можно записать, что C_3v= C₃^ C_s.

 

Лекция 3.

Сопряженные элементы и классы.

Два элемента А и В называются сопряженными, если существует элемент R, для которого выполняется соотношение:

A = R B R^-1.

Это означает, что элемент A сопряжен с Bотносительно R. Аналогичное соотношение для B будет выглядеть, как

B = R^-1A R.

Здесь Bсопряжен с Aотносительно R^-1. Множество взаимносопряженных элементов в группе называют классом. Класс может содержат один или несколько элементов. Рассмотрим сопряженные элементы группы C_3v. При помощи таблицы произведений построим таблицу сопряженных элементов.

Таблица 2. Сопряженные элементы.

	B
R	E	C3	C3 2	sv	sv¢	sv²	R-1
E	E	C3	C3 2	sv	sv¢	sv²	E
C3	E	C3	C3 2	sv²	sv	sv¢	C3 2
C3 2	E	C3	C3 2	sv¢	sv²	sv	C3
sv	E	C3 2	C3	sv	sv²	sv¢	sv
sv¢	E	C3 2	C3	sv²	sv¢	sv	sv¢
sv²	E	C3 2	C3	sv¢	sv	sv²	sv²

Каждый элемент таблицы - это элемент A = R B R^-1.

[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно.]

Первый столбец таблицы содержит только один элемент E. Т.е. элемент Е сам по себе образует класс. Каждый из столбцов C₃и C₃ ² содержит только эти элементы. Поэтому эти два элемента образуют класс. Каждый из трех столбцов s_vсодержит только элементы s_vи они также составляют класс. Элементы группы часто обозначают только классами. Например, {E, 2C₃, 3s_v}.

 

Элементы симметрии любой точечной группы можно получить из генераторов группы. Генераторами могут быть любые из 4-х элементов симметрии (C_n, s , i, S_n). По крайней мере трех из них достаточно для описании симметрии любой молекулярной системы. Систематическую классификацию систем по отвечающим им точечным группам можно провести на основе генераторов.

Если задан только один элемент симметрии, то он уже определяет точечную группу:

s - группа C_s или S₁.

i - C_i или S₂.

E - специальный случай, группа C₁.

C_n - обозначаются как и оси. Эти группы часто называют аксиальными.

S_n - обозначаются как и зеркально-поворотные оси. Определены только для четных n.

Все остальные точечные группы порождены более, чем одним генератором. Аксиальные точечные группы являются подгруппами этих групп.

Системы только с одной осьюC_n обладают не более, чем одним дополнительным генератором. Эти генератором может быть только плоскость симметрии. В зависимости от типа плоскостиs_vили s_hполучаем два типа групп: C_nv или C_nh.

У групп, имеющих более одной оси дополнительными могут быть только оси C₂ , перпендикулярные главной оси C_n. Одну из этих осей можно выбрать в качестве генератора, используемого вместе с главной осью C_n. Группы имеющие два генератора C_n и C₂ обозначаются D_n.

Группы, имеющие дополнительно к осям C_n и C₂, еще один генератор - плоскость s_h( перпендикулярна главной оси) или s_d(биссектриальная между осями C₂ ) - обозначаются как D_nh или D_nd, соответственно.

Тетраэдрические группы.

Группа T - генераторы оси C₃ и C₂. Ось C₃ совпадает с диагональю куба, а ось C₂ проходит через центры противоположных граней куба. Оси C₃ и C₂ не являются взаимно-перпендикулярными.

Группа T_d получается из группы T при введении еще одного генератора S₄. Так как S₄² =C₂, то для построения операций симметрии достаточно двух генераторов C₃ и S₄.

Группа T_h получается из группы T при введении еще одного генератора i. Т.е. генераторы оси C₃, C₂ и инверсия i.

Октаэдрические группы.

Группа O - генераторы оси C₃ и C₄. Ось C₃ совпадает с диагональю куба, а ось C₄ проходит через центры противоположных граней куба. Оси C₃ и C₄ не являются взаимно-перпендикулярными.

Группа O_h получается из группы O при введении еще одного генератора i. Т.е. генераторы оси C₃, C₄ и инверсия i.

Генераторы и обозначения групп можно кратко представить в виде таблицы 3.

Таблица 3.

Генераторы	Группа	Генераторы	Группа	Генераторы	Группа
{Cn}	Cn	{Cn, C2}	Dn	{C3xyz, S4z}	Td
{Sn}	Sn	{Cn, C2, sd}	Dnd	{C3xyz,C2z,i}	Th
{Cn, sv}	Cnv	{Cn, C2, sh}	Dnh	{C3xyz, C4z}	O
{Cn, sh}	Cnh	{C3xyz, C2z}	T	{C3xyz,C4z,i }	Oh

 

Рассмотрим на примере группы D_3d построение элементов симметрии на основе ее генераторов. Первым генератором является элемент C₃, образующий циклическую группу с элементами {E, C₃, C₃ ² }. Сначала формируется смежный класс циклической группы по отношению к одному из генераторов. В группе D_3d второй генератор - ось C₂. Смежным классом по отношению к нему являются три оси второго порядка:

{E, C₃, C₃ ² }С₂ = {С₂, C₂', C₂"}.

Оси второго порядка повернуты относительно друг друга на 120^о. В результате получим расширенную подгруппу D₃ ({E, 2C₃, 3C₂}). Затем образуем смежный класс подгруппы D₃ по отношению к плоскости s_d. Произведение подгруппы C₃ c s_d дает 3 плоскости s_d, расположенные друг относительно друга под углом 120^о. Произведение осей C₂ c s_d дают элементы S₆, S₆ ³ (или S₂, или i ) и S₆⁵ . Это произведение можно проиллюстрировать на рисунке:

Матричные представления генераторов.

 

.p/n - угол относительно оси ОХ.

Непрерывные точечные группы.

 

Линейные молекулы обладают цилиндрической симметрией и имеют бесконечное число осей симметрии. Поворот на бесконечно малый угол обозначается как C_¥. Наличие осей C_¥ требует бесконечного числа плоскостей s_v. Соответствующая группа обозначается как C_¥v. Если существует бесконечное число осей C₂, перпендикулярных C_¥, то группа обозначается D_¥h.

Самая высокая симметрия трехмерной системы - сферическая. Группа описывающая сферическую симметрию R(3), генераторами которой являются 3 любые взаимоперпендикулярные оси. Группа R_h(3) возникает из группы R(3) при добавлении еще одного генератора - операции инверсии. Все остальные точечные группы являются подгруппами групп R(3) или R_h(3).

 

 

Лекция 4.

Отображения, морфизмы.

 

Часто бывает полезно представить элементы некоторой группы другими величинами, удовлетворяющими той же таблице произведений, что и заданная группа. Это означает, что данная группа отображается в новую группу, причем каждый элемент в первоначальной группе имеет образ в новой. При этом совсем не обязательно, чтобы различные элементы в первоначальной группе имеют различные образы в новой. Если различные элементы одной группы имеют различные образы в другой группе, то эти группы называются изоморфными. В противном случае - гомоморфными. В качестве примера рассмотрим отображения группы C₄:

C4	E	C4	C2	C42
		-1		-1
		i	-1	-i
		-i	-1	i

 

Если в качестве группового произведения принять обычное умножение, то элементы каждого из 4-х отображений образуют группу. Первая группа имеет порядок 1, вторая - 2, две последние - 4. В первом случае 4 элемента первой группы отображаются в один, во втором два в один. Т.о. первые два - гомоморфизмы. В двух последних различным элементам первоначальной группы соответствуют различные образы в отображениях. Т.о. эти группы изоморфны.

Рассмотрим вновь молекулу NH₃ и каждому элементу симметрии поставим в соответствие матрицу преобразования декартовых координат атомов.

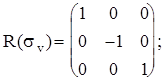
Матрицы, соответствующие операциям s_v¢ и s_v² , можно получить из произведения матриц R(C₃ ²)R(s_v) и R(C₃)R(s_v), соответственно, или через матрицу генератора s_dпри (p/n)=120^oи (p/n)=-120^o.

Из произведений матриц можно составить таблицу полностью идентичную таблице произведений элементов точечной группы C_3v. Т.о. этот набор матриц образует группу изоморфную точечной группе C_3v. Если существует множество матриц, представляющих собой группу и имеющих такую же таблицу произведений что и данная группа, то говорят, что эти матрицы порождают матричное представление (или просто представление) группы. Группа матриц, являющаяся представлением данной группы, не обязательно должна быть изоморфна последней. Матрицы могут быть одномерными, двумерными, трехмерными и т.д. Они могут быть действительными, комплексными и мнимыми. Единственное требование - они должны быть гомоморфны рассматриваемой группе и удовлетворять таблице произведений группы. Может существовать бесконечное множество возможных представлений. В том случае, если группа матриц изоморфна точечной группе, то они образуют точное представление группы.

Однако подробное и полное изложение теории представлений является предметом отдельного специального курса. Здесь речь пойдет лишь о тех понятиях теории представлений, которые будут необходимы для практического применения теории групп. Одной из основных задач, возникающих при поиске представлений групп, является определение так называемых неприводимые представлений. Неприводимые представления - матричные представления самой низшей размерности, которые нельзя преобразовать друг в друга. Неприводимые представления обладают следующими свойствами.

Если неприводимые представления одномерны, то они сами образуют группу.

Сумма квадратов размерностей неприводимых представлений равна порядку группы.

Число различных неприводимых представлений группы равно числу ее классов.

Рассмотрим группу C₂ {E, C₂}. Матрицы соответствующие операциям симметрии имеют вид:

Эти матрицы образуют представление группы C₂. Однако оно не является самым простым. Поскольку матрицы диагональны, то x, y и z координаты преобразуются независимо друг от друга. Рассматривая только эти компоненты получим три независимых отображения группы C₂:

	E	C2
G(x)		-1
G(y)		-1
G(z)

 

Т.к. базисные вектора декартовой системы взаимноортогональны, то эти отображения взаимонезависимы. В отдельности - это неприводимые представления группы C₂. Числа, выражающие эти представления, называются характерами. Характер - след матрицы, соответствующей данной операции симметрии. Здесь представления G(x) и G(y) совпадают и , следовательно, у группы C₂ есть только два одномерных неприводимых представления. Таблица характеров неприводимых представлений для группы C₂ имеет вид:

С2	E	C2
A
B		-1

Таблица характеров включает в себя характеры для различных операций в каждом неприводимом представлении.

Рассмотрим группу C₃ {E, 2C₃}. Матрицы соответствующие операциям симметрии имеют вид:

Матрицы, соответствующие операциям поворота, недиагональны. Т.о. x и y компоненты взаимозависимы. Следовательно из нельзя использовать отдельно для построения представлений. Однако z-компонента порождает независимое представление. Еще одно представление дают квадратные матрицы 2-го порядка, описывающие взаимное преобразование координат x и y. Это будет также неприводимое представление. Таблицу характеров можно записать двумя способами. Первый - через следы матриц:

С3	E	2C3
A
E		-1

Второй способ - диагонализация матриц. В результате приведения матриц, описывающих повороты, к диагональному виду получим новые матрицы:

Два первых диагональных элемента являются комплексносопряженными. Двумерное представление можно разложить на два мнимых одномерных и таблицу характеров записать в виде:

С3	E	C3	C3 2
A
E

Порядок группы - 3. Размерности представлений 1²+ 1²+ 1²= 3. Для циклических групп рассматриваются мнимые представления.

Группа C_2v {E, C₂, s_v^{x z}, s_v^{y z}}. Матрицы операций симметрии:

Матрицы диагональны, т. о. получим таблицу представлений:

	E	C2	svx z	svy z
G(x)		-1		-1
G(y)		-1	-1
G(z)

Однако в соответствии со свойствами представлений должно быть 4 неприводимых представления. Четвертое находится на основании свойства: G(a)´ G(b)= G(c) [a_i´b_i=c_i]. Т.о.

G(z)´ G(x)={1 -1 1 -1 }=G(x)

G(z)´ G(y)={1 -1 -1 1 }=G(y)

G(x)´ G(y)={1 1 -1 -1 } ® новое представление.

В результате таблица характеров для группы C_2v примет вид:

	E	C2	svx z	svy z
A1
A2			-1	-1
B1		-1		-1
B2		-1	-1

В итоге мы имеем:

группа C₂ - 2 представления - 2 вектора в двухмерном пространстве;

группа C₃ - 1 одномерное и 1 двухмерное представления - 3 вектора в

трехмерном пространстве;

группа C_2v - 4 одномерных представления - 4 вектора в четырехмерном

пространстве.

Т.о. неприводимые представления описывают элементы симметрии в n-мерном пространстве, построенном на системе n независимых базисных векторов.

 

Лекции 5-6.

Построение таблиц характеров.

Неприводимые представления и характеры циклических точечных групп можно построить непосредственно, руководствуясь следующими правилами:

1. Для групп C_n при четном n существует представление A и B (одномерные) и множество двумерных представлений E_k с k=1,2,. . ., (n/2)-1.

2. Если n нечетное, то представления B не существует, а индекс k для E_kпринимает значения k=1,2,. . ., (n-1)/2.

Характеры для пар вырожденных представлений E_k равны e^(2pi/n)jkи e^(-2pi/n)jk, где k - индекс E_k, аj определяется элементом симметрии C_n ^j .

3. Характеры представлении A и B можно получить как особые случаи E_k с k=0или(n/2), соответственно. Т.о. представлениеA - полносимметричное с характерами c=1. Поскольку e^(2pi/n)0= e⁰=1. Для B имеем

e^(2pi/n)jn/2= e^jpi= cos(jp) - isin(jp) = cos(jp) , т.к. sin(jp)=0 и т.о.

c(B)= cos(jp)=±1( +1 при четных j и -1 при нечетных j).

 

Например, для группы C₃ имеем представления A и E₁ или просто E и таблицу характеров.

С3	E	C3	C3 2
A
E

e^4pi/3= e^-2pi/3; e^-4pi/3= e^2pi/3; т.к. 4p/3=240^о=-2p/3=-120^о.

Действительное представление получается при использовании формулы Ейлера:

₊ ^- .

Таким образом для C₃ получим.

С3	E	C3	C3 2
A
Eкомпл.
G1+G2		2cos(2p/3)	2cos(2p/3)
Eдействит.		-1	-1

 

Рассмотрим группу C₆:

В соответствии с правилами 1-3 имеем представления A, B, E₁ и E₂ и обозначая e^2pi/6=e, а комплексносопряженную как e^* получим следующую таблицу характеров:

С6	E	C6	C6 2 =C3	C63 =C2	C64 =C32	C65
A
B		-1		-1		-1
E1
E2

Учитывая, что e^*=cos(60^o)+isin(60^o) и

e²=cos(120^o)-isin(120^o)=-cos(60^o)-isin(60^o)=-(cos(60^o)+isin(60^o))=-e^* и т.д. таблицу характеров можно записать в виде:

С6	E	C6	C3	C2	C3 2	C65
A
B		-1		-1		-1
E1
E2

В действительном виде таблица характеров запишется как:

С6	E	2C6	2C3	C2
A
B		-1		-1
E1			-1	-2
E2		-1	-1

 

Таблицы характеров остальных подгрупп можно построить из прямого или полупрямого произведения подгрупп. Рассмотрим процедуру построения, например, для группы D_2h=D₂´C_s. На первом этапе используя операции симметрии подгрупп находим операции симметрии группы и это отобразим в виде таблицы (1)

	D2
Cs	E	C2z	C2y	C2x
E	E	C2z	C2y	C2x
sxy	sxy	i	syz	sxz

 

(1)

 

 

Т. о. для группы D_2h имеем 8 операций симметрии. Можно, показать, что каждая из них образует отдельный класс.

На втором этапе зная представления подгрупп получим таблицу произведений неприводимых представлений подгрупп (2):

	D2
Cs	A1	B1	B2	B3
A¢	A¢A1	A¢B1	A¢B2	A¢B3
A²	A²A1	A²B1	A²B2	A²B3

(2)

 

 

Cs	E	sxy
A¢
A²		-1

В таблице (2) получено 8 представлений группы. Число представлений равно числу классов группы. Следовательно все эти представления - неприводимые. Для нахождения характеров неприводимых представлений группы нужно знать таблицы характеров неприводимых представлений подгрупп.

D2	E	C2z	C2y	C2x
A1
B1			-1	-1
B2		-1		-1
B3		-1	-1

На третьем этапе для каждой пары из табл. 2 найдем произведения характеров соответствующих неприводимых представлений подгрупп и результаты представим в виде 8-ми таблиц похожих по форме на табл. 1.

D2

D2

Cs

E

C2z

C2y

C2x

Cs

E

C2z

C2y

C2x

A1

(3)

A1

(7)

A¢

A²

E

sxy

-1

-1

-1

-1

-1

	D2			D2
Cs	E	C2z	C2y	C2x		Cs	E	C2z	C2y	C2x
	B1	(4)		B1	(8)
	A¢			-1	-1		A²			-1	-1
E				-1	-1					-1	-1
sxy				-1	-1		-1	-1	-1

	D2			D2
Cs	E	C2z	C2y	C2x		Cs	E	C2z	C2y	C2x
	B2	(5)		B2	(9)
	A¢		-1		-1		A²		-1		-1
E			-1		-1				-1		-1
sxy			-1		-1		-1	-1		-1

	D2			D2
Cs	E	C2z	C2y	C2x		Cs	E	C2z	C2y	C2x
	B3	(6)		B3	(10)
	A¢		-1	-1			A²		-1	-1
E			-1	-1					-1	-1
sxy			-1	-1			-1	-1			-1

Значения характеров в ячейках табл. 3-10 соответствуют элементам симметрии размещенным в аналогичных ячейках табл. 1.

Таблицы 3-10 можно объединить в одну таблицу характеров группы D_2h. При этом для обозначения произведений представлений в табл. 2 используются определенные правила, которые будут разобраны нами на следующих занятиях.

Таблица характеров для группы D_2h.

D2h	E	C2z	C2y	C2x	sxy	i	syz	sxz
Ag
B1g			-1	-1			-1	-1
B2u		-1		-1		-1		-1
B3u		-1	-1			-1	-1
Au					-1	-1	-1	-1
B1u			-1	-1	-1	-1
B2g		-1		-1	-1		-1
B3g		-1	-1		-1			-1

В случае полупрямого произведения процедура построения таблицы характеров несколько усложняется. Рассмотрим группу C_3v=C₃ÙC_s. Найдем операции симметрии группы (табл. 11):

	Cs
C3	E	sv
E	E	sv
C3	C3	sv¢
C32	C32	sv²

 

(11)

 

Если по вертикали записаны элементы симметрии инвариантной подгруппы, то столбцы будут содержать классы группы. Для группы C_3v имеем 3 класса {E, 2C₃, 3s_v }и, следовательно, должно быть 3 неприводимых представления. Составим таблицу произведения неприводимых представлений подгрупп.

	Cs
С3	A¢	A²
A	AA¢	AA²	(12)
E

В табл. 12 есть 6 пар произведений, но в группе С_3v должно быть только три неприводимых представления. При этом нужно учесть, что произведения полносимметричного представления (А) группы C_3v дают всегда неприводимые представления. Т.о. произведения AA¢ и AA² в табл. 12 - два неприводимых представления. Очевидно, 4 оставшихся являются зависимыми.

Получим характеры представлений.

AA¢	Сs		AA²	Сs
С3	E	sv			E	sv
	A¢			A²
	A				A		-1
E				(13)			-1	(14)
С3							-1
C32							-1

 

E(1)A¢	Сs		E(1)A²	Сs
С3	E	sv			E	sv
	A¢			A²
	E(1)				E(1)		-1
E				(15)			-1	(16)
С3	e	e	e		e	e	-e
C32	e*	e*	e*		e*	e*	-e*

 

E(2)A¢	Сs		E(2)A²	Сs
С3	E	sv			E	sv
	A¢			A²
	E(2)				E(2)		-1
E				(17)			-1	(18)
С3	e*	e*	e*		e*	e*	-e*
C32	e	e	e		e	e	-e

Для нахождения третьего представления проведем усреднение характеров элементов по классам для каждого из 4-х зависимых представлений. Получим:

	E	2C3	3sv		E	2C3	3sv
E(1)A¢		(e+e*)/2	(1+e+e*)/3	E(1)A²		(e+e*)/2	-(1+e+e*)/3
	(1	-1/2	0)		(1	-1/2	0)
E(2)A¢		(e*+e)/2	(1+e*+e)/3	E(2)A²		(e*+e)/2	-(1+e*+e)/3
	(1	-1/2	0)		(1	-1/2	0)
Cумма		-1		Cумма		-1

Т.о. получены два совершенно одинаковых представления и это будет в группе C_3v - третье представление. Таблица характеров будет выглядеть следующим образом:

C3v	E	2C3	3sv
A1
A2			-1
E		-1

Таблица характеров для группы T_d.

T_d = D₂ ^ C_3v

Элементы симметрии группы T_d.

	C3v
D2	E	2C3	3sv
E	E	2C3	3sd
C2z	C2z	2C3¢	3sd¢
C2y	C2y	2C3²	3S4
C2x	C2x	2C3²¢	3S4¢

s_v - в тетраэдре соответствует s_d.

Т.о. имеется 5 классов T_d={E, 3C₂, 8C₃, 6s_d, 6S₄}.

Таблица произведений представлений:

	C3v
D2	A1	A2	E
A1	A1A1	A1A2	A1E
B1	B1A1	B1A2	B1E
B2	B2A1	B2A2	B2E
B3	B3A1	B3A2	B3E

Произведения A₁A₁, A₁A₂, A₁E образуют три неприводимых представления.

Остальные 9 - зависимые и из нужно получить еще два неприводимых представления. Для нахождения этих представлений построим таблицу произведений характеров соответствующих неприводимых представлений подгрупп.

	C3v
	A1	A2	E
D2	E	2C3	3sv	E	2C3	3sv	E	2C3	3sv
						-1		-1
B1							-1		-1
							-1		-1
	-1	-1	-1	-1	-1	-1		-2
	-1	-1	-1	-1	-1	-1		-2
B2							-1		-1
	-1	-1	-1	-1	-1	-1		-2
							-1		-1
	-1	-1	-1	-1	-1	-1		-2
B3							-1		-1
	-1	-1	-1	-1	-1	-1		-2
	-1	-1	-1	-1	-1	-1		-2
							-1		-1

Одинаковым фоном выделены характеры элементов симметрии, относящиеся к одному классу группы T_d.

Просуммируем для зависимых представлений характеры по классам элементов симметрии (классы в табл. выделены одним фоном) и усредним. В результате получим:

	E	3C2	8C3	6sd	6S4
B1A1	(1)	(1-1-1)/3 -1/3	(1+1-1-1)/4	(1+1)/2	(-1-1)/2 -1
B2A1		-1/3
B3A1		-1/3
S		-1			-1
B1A2		-1/3		-1
B2A2		-1/3
B3A2		-1/3
S		-1		-1
B1E		-2/3
B2E		-2/3
B3E		-2/3
S		-2

Последнее представление - сумма двух первых представлений. Т.о в группе T_d имеется еще два независимых неприводимых трехмерных представления T₁ и T₂.

 

 

Уравнение, описывающее свойства атомов и молекул, это уравнение Шредингера:

где - оператор Гамильтона, Е- энергия системы,

Y-волновая функция.

Полная волновая функция: Y_т=Y_эл.Y_кол.Y_вр.Y_пост.

Y_эл. - электронная волновая функция,

Y_кол. - колебательная волновая функция,

Y_вр. - вращательная волновая функция,

Y_пост. - поступательная волновая функция,

- инвариантен по отношению к операциям симметрии и т.о. преобразуется всегда по полносимметричному представлению точечной группы.

Волновая функция, согласно теореме Вигнера, преобразуется по неприводимому представлению. Причём это относится как к Y_т, так и Y_эл.,Y_кол., Y_вр., Y_пост. Волновая функция системы, согласно принципу Паули, должна быть антисимметрична по отношению к перестановке любых двух электронов. На самом деле этот принцип имеет гораздо более общий характер - волновая функция для любой системы фермионов (е, n^o, p - частицы с полуцелым спином) должна быть антисимметричной. Это требование налагает сильные ограничения на систему. Молекула или атом – это система, состоящая из ядер и электронов. Симметрия ядер определяется пространственной (точечной) группой симметрии, а симметрия электронов – группой перестановок n- эквивалентных частиц. Т. о. полная группа имеет вид:

G = G_s · S(n), где

G_s- точечная группа,

S(n) - группа перестановок.

Характеры элементов в полной группе можно получить из рассмотрения перестановочных свойств. В случае фермионов требование антисимметричности означает, что перестановочное представление группы должно быть сопряжённым к соответствующему представлению S(n), т. к. только произведение представления с ему сопряжённым содержит полностью антисимметричное представление. В группе S(n) в сопряжённом представлении строки и столбцы, соответствующей диаграммы Юнга, переставлены местами. Разрешёнными представлениями S(n) для n- частиц являются представления, имеющие 2j+1 строк в диаграмме Юнга, где j – собственный угловой момент частицы. Для электрона j=½. Т.о. в разрешённых схемах Юнга для системы из электронов должно быть не более двух строк. Например, для системы из четырёх электронов имеем:

 

Перестановочное представление (S(4))

Пространственное представление (Gs)

[4]

[14]

[3,1]

[2,12]

[22]

[22]

 

Электронам в диаграмме Юнга для S(4) в первой строке приписывают значения спина ½, в нижней (-½).