Учебные вопросы

Москва

Дисциплина: Эконометрика

КОНСПЕКТ ЛЕКЦИИ № 2

на тему: «Модель множественной линейной регрессии»

 

 

Автор: С.В. Суржик, доцент, к.э.н., доцент

 

 

 

 

1. Задача построения множественной линейной регрессии.

2. Оценка качества модели множественной линейной регрессии.

3. Прогнозирование по модели множественной линейной регрессии.

1.В общем случае зависимая переменная у может быть функцией нескольких переменных: х₁, х₂, …, х_m.

В каждом наблюдении (i) получают совокупность значений независимой переменной: х_i1, x_i2 ,…, x_im и совокупность значений зависимой переменной у_i. Итак, допустим,

y_i = α₁x_i1 + α₂x_i2 +…+α_mx_im + ε_i. (1)

Введем матричные обозначения.

Пусть {αj}, j = 1,…, m – вектор неизвестных параметров; Y = {y_i}, i =1,...,n

- вектор зависимой переменной; X = (x_ij) – матрица независимых переменных размером nm; ε = {ε_i}- вектор ошибок.

Тогда линейная модель (1) перепишется в виде

Y = Xα + ε (2)

Относительно ошибок ε сделаем следующие предположения:

1) возмущение ε является случайной величиной;

2) М(ε) = 0;

3) Д(ε) = const;

4) последовательные значения ε не зависят друг от друга;

5) матрица Х состоит из линейно-независимых векторов-столбцов.

Последнее обстоятельство эквивалентно тому, что ранг матрицы Х равен m, а это, в свою очередь, означает, что |X′X| ≠ 0, т.е. матрица X′X обратима (X′ - транспонированная для Х).

Матрица Х не содержит ошибок.

Таким образом, для определения вектора анеобходимо по данным наблюдений найти матрицу, обратную к матрице Х′X, и вектор Х′Y:

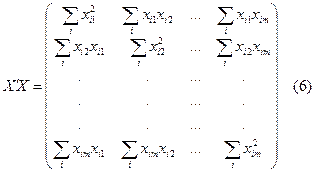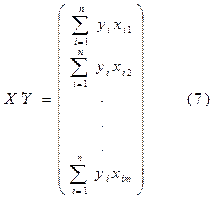
Обычно предполагается, что уравнение регрессии имеет свободный член, т.е. а₀. Чтобы получить оценку этого параметра, расширим матрицу (6), введя в нее переменную Х_i0 = 1.

Тогда матрицу Х в развернутом виде можно записать так:

 

 

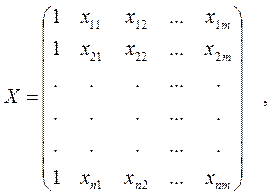Тогда

 

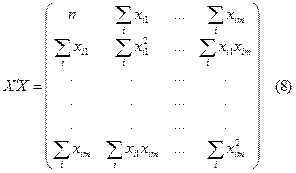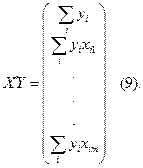И

 

В частном случае, когда m=2, имеем