АЛГОРИТМ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ БИНС

ЛЕКЦИЯ №8

Алгоритм определения параметров БИНС можно представить в виде 4-х субалгоритмов:

1. Алгоритм определения начальной матрицы ориентации.

Здесь вычисляются начальные значения элементов матрицы направляющих косинусов, определяющей взаимное положение связанной с ЛА и геометрической системой координат. Алгоритмы используются при начальной выставке БИНС на Земле. Выставка осуществляется методом векторного согласования по измерениям двух неколлинеарных векторов измерительными элементами БИНС (акселерометрами, гироскопами) – вектора абсолютной угловой скорости вращения ЛА, равного угловой скорости вращения Земли 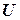, и вектора ускорения свободного падения .

2. Алгоритм вычисления матрицы взаимной ориентации базиса, связанного с ЛА и географического.

Этот алгоритм может быть построен несколькими существенно разными способами, выбор которых определяется особенностями гироскопов БИНС и спецификой конкретной навигационной задачи. Наиболее часто используются два способа.

Алгоритм определения параметров БИНС можно представить в виде 4-х субалгоритмов:

Первый способбазируется на решении матричного модифицированного уравнения вращения Пуассона:

 

,

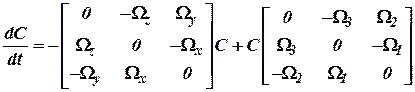(32)

 

где 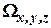- проекции абсолютной угловой скорости вращения географической системы координат, определяемые как:

 

,

(33)

 

- абсолютные угловые скорости ЛА, измеряемые гироскопами, установленными жестко на его корпусе.

Второй способпостроения алгоритма ориентации базируется на использовании промежуточных параметров ориентации.

При создании БИНС наиболее часто в качестве таковых используются параметры Родрига-Гамильтона (кватернионы). Матрица пересчета из связанной в географическую систему координат получается путем перемножения двух матриц, из которых одна пересчитывается в связанных в инерциальные оси – вторая из инерциальных в географические. Каждая из двух матриц вычисляется на основе параметров Родрига-Гамильтона, которые в свою очередь определяются численным алгоритмом второго порядка, построенным на основе метода последовательных приближений Пикара:

 

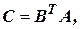
.	(34)
,

 

,

 

,

 

,

 

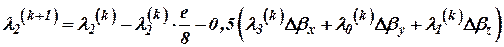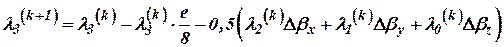где ,

;;,

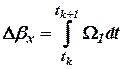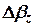, , - приращения интегралов от проекций абсолютной угловой скорости поворота объекта на оси чувствительности гироскопов (показания гироскопов БИНС, измеряющих не проекции угловых скоростей, а приращение углов поворота вокруг своих осей чувствительности).

 

,

 

;

 

;

 

;
,

 

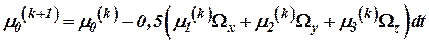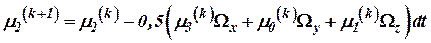где , , 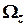- проекции абсолютной угловой скорости географического базиса на его оси (2).

К преимуществам этого метода построения матрицы ориентации относится гарантированная ортогональность матрицы ориентации, вычисленной по соотношениям (34). Кроме этого практика показывает, что вычисление с использованием параметров Родрига-Гамильтона дает наименьшие вычислительные затраты по сравнению с другими методами при условии обеспечения одинаковых точностных характеристик. Вместе с тем, определение матрицы С через параметры Родрига-Гамильтона приводит к необходимости решения двух однотипных систем дифференциальных уравнений 4-го порядка каждая.

3. Алгоритм вычисления угловых параметров ориентации ЛА относительно географической системе координат (вычисление истинного курса , крена , тангажа ):

 

,

 

,

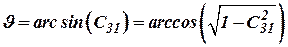(35)

где - элементы введенной выше матрицы .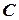

4. Алгоритмы пересчета сигналов, полученных с акселерометров в географическую систему координат для использования в навигационном алгоритме:

.

(35)

 

Приведенная совокупность соотношений (26)…(36) представляет собой замкнутую систему уравнений, параметров ориентации ЛА.

Совокупность любого из приведенных уравнений определения матрицы 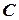и углов , , образуют алгоритм ориентации БИНС. Выбор конкретного алгоритма определения матрицы 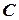зависит от поставленной задачи и доступных ресурсов.