Вопросы для самопроверки
- Что называется стержнем?
- Какой вид нагружения стержня называются осевым растяжением (сжатием)?
- Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
- Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
- Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?
- Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
- Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются?
- Получите формулу нормальных напряжений при растяжении-сжатии? Какие предпосылки используются при выводе этой формулы?
- Как записывается условие прочности бруса при растяжении (сжатии)? Какие виды задач решаются с помощью условия прочности?
- В каких единицах измеряется напряжение?
- Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
- Как назначаются знаки продольной силы и нормального напряжения?
- Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?
- Раскройте понятие эпюр продольных сил, нормальных напряжений и перемещений. Для чего они строятся?
- Что показывает эпюра продольной силы?
- Что представляют собой эпюры внутренних силовых факторов? С какой целью их строят?
- Опишите технику построения эпюры продольных сил в брусе, загруженном несколькими сосредоточенными силами по оси бруса?
- Как вычислить значение продольной силы в произвольном поперечном сечении бруса?
- Как вычислить напряжения в поперечном сечение бруса при растяжении и сжатии? Как они распределены по поперечному сечению?
- Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?
- Как определяется удлинение призматического бруса от собственного веса?
- Какое влияние оказывает собственный вес стержня при проектирования сооружения?
- Что понимается под брусом равного сопротивления?
- Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?
- Какие деформации бруса называются абсолютными и какие относительными?
- Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?
- Опишите технику определения продольных и поперечных деформаций бруса при растяжении-сжатии?
- Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (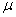
= 0,25)
- Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?
- Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
- Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?
- Относительные деформации и перемещения.
- Что понимается под жесткостью при растяжении или сжатия стержня?
- Принципы расчета на жесткость.
- Типы задач при расчетах на жесткость.
- Примеры влияния жёсткости на работоспособность конструкции.
- Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.
- Что происходит с поперечными размерами стержня при его растяжении (сжатии)?
- Что характеризует коэффициент поперечной деформации?
- Что такое коэффициент Пуассона? В каких пределах он изменяется?
- Как определяется коэффициент Пуассона?
- Какая разница между статически определимой и статически неопределимой стержневой системой?
- Какие системы называют статически неопределимыми? Как установить степень статической неопределимости системы?
- В какой последовательности рассчитывают статически неопределимые системы?
- Сколько уравнений статики нужно составить для системы сил, лежащих на одной прямой?
- Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости, но сходящихся в одной точке?
- Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости и не сходящихся в одной точке?
- Какое влияние оказывает на стержневую статически неопределимую системы изменение температуры?
- Как учитываются в статически неопределимых стержневых системах монтажные напряжения?
- Как ведется расчет статически неопределимых систем по методу разрушающих нагрузок?
- Объясните метод расчета статически неопределимых стержневых систем по предельному состоянию?
- Во сколько раз (примерно) поперечная деформация меньше продольной при осевом растяжении (сжатии) стальных стержней?
- При проведении испытаний были получены различные значения коэффициента Пуассона для стали: 0,15; 0,28; 0,4. Укажите, какие значения ошибочны?
- Вычислите продольную силу, возникающую в поперечном сечении растянутого стержня, если нормальные напряжения в этом сечении равны 140 МПа, а его площадь составляет 100 мм2?
- Определение нормальных и касательных напряжений на наклонных площадках при растяжении – сжатии. Вывод формулы.
- Вывести формулу определения нормальных напряжений при растяжении-сжатии.
- Укажите деформированное состояние стержня, нагруженного осевой силой, если его поперечные размеры увеличились?
1) стержень растянут;
2) стержень сжат.
- На рисунке изображён стержень, находящийся под действием растягивающей силы.
Большие напряжения возникнут в точке
1) C;
2) D?
- Выберите формулу закона Гука при растяжении (сжатии)?
1) 
;
2) 
;
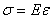3) 
;
4) 
.
- Какие внутренние усилия возникают при растяжении (сжатии)?
1) поперечная сила,
2) продольная сила.
- Что связывает закон Гука при растяжении (сжатии)?
1) продольную и поперечную силу,
2) напряжение и деформацию.
- Что является характеристикой жесткости при растяжении?
1) модуль упругости первого рода,
2) модуль упругости второго рода.
- Условие жесткости:
1) рабочее напряжение должно быть меньше временного сопротивления;
2) относительная деформация: линейная 
, угловая 
;
3) относительная линейная и угловая деформации одинаковы численно.
- При растяжении (сжатии):
1) 
;
2) 
;
3) 
, 
.
- Три вида задач из условия жесткости:
1) определение линейных размеров;
2) проверка на условие жесткости; определение размеров сечения; определение максимально допустимых размеров;
3) определение изменения объема конструкции.
- Выбор сечения из условия жесткости
1) сечение должно удовлетворять как условию прочности, так и жесткости;
2) сечение должно удовлетворять только условию прочности;
3) сечение должно удовлетворять только условию жесткости.
- При расчетах на жесткость получают:
1) гибкость стержня;
2) твердость материала;
3) линейные и угловые деформации.
- Какие напряжения возникают в поперечном сечении при растяжении (сжатии)?
1) сжимающие,
2) касательные,
3) продольные,
4) нормальные,
5) изгибающие.
- По формуле 
определяют:
1) напряжение;
2) прочность;
3) деформацию;
4) твёрдость;
5) коэффициент мягкости.
- Условие прочности при растяжении – сжатии имеет вид:
1) 
;
2) 
;
3) 
;
4)
- По какой из формул определяется коэффициент запаса прочности для пластичного материала?
1) 
;
2) 
;
3) 
;
4) 
- По какой из формул находятся касательные напряжения в любом сечении сжатого стержня?
1) ;
2) 
;
3) 
;
4) 
.
- По какой из приведённых формул определяются нормальные напряжения при растяжении:
1) ;
2) 
;
3) ;
4)
.
- В каких единицах измеряются нормальные и касательные напряжения?
1) Н/м3;
2) МПа;
3) кН/м;
4) нет правильного ответа.
- Закон Гука при растяжении–сжатии имеет вид:
1) ;
2) 
;
3) ;
4)
- Разделив абсолютное удлинение стержня на его относительное удлинение, что мы получим:
1) коэффициент Пуассона;
2) модуль Юнга;
3) первоначальную длину стержня;
4) нет правильного ответа.
- Два сжатых стержня, равные по размерам, имеют разную жёсткость (у I-го она больше). Различны ли их модули Юнга?
1) нет. 
;
2) да. ;
3) да. 
;
4) да. 
.
- Условие жёсткости при растяжении – сжатии:
1) 
;
2) 
;
3) 
;
4)
- Какие напряжения возникают в поперечном сечении при центральном растяжении – сжатии?
1) касательные;
2) нормальные;
3) 
и 
;
4) 
и 
.
- Полная деформация образца состоит из:
1) упругой и пластической;
2) пластической;
3) только упругой.
- Если продольная сила N вызывает сжатие, то она считается:
1) положительной;
2) отрицательной;
3) нет правильного ответа.
- Какой зависимостью связано полное напряжение с составляющими и ?
1) 
;
2) 
;
3) 
;
4) нет правильного ответа.
- Отношение относительной поперечной деформации к относительной продольной деформации называется:
1) коэффициентом Пуассона;
2) модулем упругости;
3) первоначальной длиной стержня;
4) абсолютным удлинением.
- Известно, что материалы по-разному работают на растяжение – сжатие. У каких материалов меньше различий?
1) у пластичных;
2) у хрупких;
3) нет различия.
- По какой из формул определяется коэффициент запаса прочности для хрупкого материала?
1) 
;
2) 
;
3) 
;
4) 
.
- Как вычисляются нормальные напряжения в наклонных сечениях центрально растянутого, или сжатого бруса?
1) 
;
2) ;
3) 
;
4) .
- Какие перемещения получают поперечные сечения стержня при растяжении–сжатии?
1) линейные;
2) угловые;
3) линейные и угловые.
- График, показывающий изменение величины напряжений по высоте или ширине поперечного сечения называют:
1) эпюрой напряжений;
2) эпюрой моментов;
3) эпюрой сил.
- Величина коэффициента Пуассона колеблется в интервале:
1) 
;
2) 
;
3) 
;
4) 
.
- Отношение абсолютного удлинения к первоначальной длине бруса называется:
1) относительной продольной деформацией;
2) модулем упругости;
3) относительной поперечной деформацией;
4) полным удлинением .
- Указать выражение, соответствующее жёсткости сечения при растяжении–сжатии.
1)
;
2)
;
3)
;
4)
.
- Допускаемое нормальное напряжение для пластичных материалов определяется:
1) 
;
2) 
;
3) 
;
4) .
- Каким соотношением может быть выражена сила «N» через нормальные напряжения?
1) 
;
2) 
;
3) нет правильного ответа.
- Какие свойства материала характеризует коэффициент Пуассона?
1) остаточные;
2) пластические;
3) упругие.
- Абсолютное удлинение выражается формулой:
1) 
;
2) 
;
3)
;
4) нет правильного ответа.
- Сколько внутренних силовых факторов возникает в поперечных сечениях прямого бруса при центральном растяжении (сжатии)?
1) два;
2) один;
3) отсутствуют;
- Если продольная сила N вызывает растяжение, то она считается:
1) положительной;
2) отрицательной;
3) нет правильного ответа.
- Относительное удлинение определяют по формуле:
1) 
=
;
2) 
;
3) 
;
4) 
.
- Какому напряженному состоянию соответствуеткольцевое сжатие образцов по боковой поверхности ?
1) двухосное растяжение;
2) двухосное сжатие;
3) разноимённое плоское напряжённое состояние;
4)трёхосное растяжение;
5)трёхосное сжатие.
- Закон Гука определяет прямую пропорциональность между упругой деформацией и:
1) пластической деформацией;
2) скоростью приложения нагрузки;
3) коэффициентом Пуассона;
4) напряжением;
5) внутренним трением.
- Что определяютмодули упругости?
1) мягкость материала;
2) твёрдость материала;
3) жёсткость материала;
4) пластичность материала;
5) прочность материала.
- Физический смысл модулей упругости состоит в том, что они характеризуют:
1) отношение продольной относительной деформации к поперечной;
2) относительное удлинение в упругой области;
3) сопротивляемость металлов смещению атомов из положений равновесия в решётке;
4) скорость уменьшения напряжения по мере упругой деформации;
5) обратную пропорциональность между напряжением и упругой деформацией.
- Полная работа на пластическую деформацию равна:
1) 
;
2) 
;
3) 
;
4)
;
5) 
.
- Как определяются напряжения при осевом растяжении (сжатии)?
1) 
;
2) 
;
3) 
;
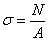4)
- Что характеризует жесткость при растяжении (сжатии)?
1) модуль упругости второго рода,
2) модуль упругости первого рода,
3) коэффициент Пуассона.
- Какие характеристики связывает закон Гука при растяжении (сжатии)?
1) силу и напряжение,
2) касательное и нормальное напряжение,
3) напряжение и деформацию.
-Что связывает поперечную и продольную деформацию при растяжении (сжатии)?
1) модуль упругости,
2) модуль сдвига,
3) коэффициент Пуассона.
-Что характеризует произведение ЕА при растяжении (сжатии)?
1) твердость материала,
2) жесткость материала,
3) жесткость стержня.
- В каких сочетаниях растянутого бруса возникают наибольшие нормальные, и в каких наибольшие касательные напряжения?
1) Наибольшие нормальные напряжения возникают в поперечных сечениях бруса. Наибольшие касательные возникают в сечениях под углом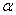 
=45°.
2) Наибольшие нормальные напряжения возникают в сечениях под углом 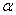=45°. Наибольшие касательные напряжения в поперечных сечениях бруса.
3) Наибольшие нормальные напряжения возникают в сечениях под углом 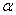=0°. Наибольшие касательные напряжения возникают под углом 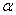=45°.
4) Наибольшие нормальные напряжения возникают в сечениях бруса под углом 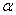=90°. Наименьшие касательные напряжения возникают под углом 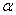=0°.
- Что называется жесткостью поперечного сечения при растяжении (сжатии)?
1) Жесткостью называется такое состояние материала, при котором деформации ниже допустимых величин.
2) Отношение 
называется жесткостью поперечного сечения.
3) Произведение 
называется жесткостью поперечного сечения.
4) Произведение называется жесткостью поперечного сечения.
- Назовите единицы измерения коэффициента Пуассона?
1) Н/м2.
2) Па.
3) безразмерная величина.
4) м/Н.
- Наибольшее по модулю напряжение равно, полагая 
1) 
2) 
3) 
4) 
- Растягиваемый стержень заменили другим с площадью поперечного сечения в два раза большей. В каком из вариантов напряжения останутся неизменными:
1) силу увеличили в 4 раза;
2) силу уменьшили в 2 раза;
3) силу увеличили в 2 раза;
4) силу уменьшили в 4 раза.
- Растягиваемый стержень заменили другим, тех же размеров, с модулем Юнга в два раза большим. В каком из вариантов относительное удлинение останется прежним:
1) силу увеличили в 4 раза;
2) силу увеличили в 2 раза ;
3) силу оставили неизменной;
4) силу уменьшили в 2 раза.
- Стержень растягивается силой F = 7,85 кН, диаметр поперечного сечения D = 10 мм. Чему равны напряжения в поперечном сечении бруса?
1) 200 МПа;
2) 100 МПа;
3) 50 МПа;
4) 120 МПа.
- Определить модуль Юнга, если D = 2см, l =2 м, F= 8 кН,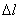 
= 0,5 мм.
1) 
МПа;
2) 
МПа;
3) 
МПа;
4) 
МПа.
- Определить допускаемое значение нагрузки [F] для стального бруса, если A=10 см2,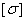 
=160 МПа
1) [F] = 32 кН;
2) [F] = 64 кН;
3) [F] = 320 кН;
4) [F] = 48 кН.
- Какое напряжение возникает при затяжке болта, если l = 160 мм, 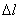= 0,12 мм, 
МПа ?
1) 150 МПа;
2) 100 МПа;
3) 50 МПа;
4) 120 МПа.
- Какую наибольшую нагрузку может выдержать деревянный столб сечением 16х16см2 при сжимающем нагружении не более 10 МПа?
1) 25,6 кН;
2) 256 кН;
3) 38,7 кН;
4) 0,387 кН.
- Проволока длиной l=10 м под действием растягивающей силы F=700 Н удлинилась на 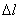=11 мм. Определить модуль упругости Е, если A=3,1 мм2.
1) 
МПа;
2) 
МПа;
3) 
МПа.
- Определить общее изменение длины бруса, если А=10 см2, l=1 м, МПа, F = 20 кН.
1) 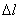= 0,3 мм;
2) 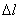= 0,45 мм;
3) 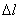= 0,58 мм;
4) 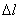= 4,5 мм.
- Определить напряжение в канате, состоящем 40 проволок, каждая диаметром D=2 мм, при растяжении нагрузкой F = 20 кН
1) =122 МПа;
2) =159,2 МПа;
3) =66,4 МПа;
4) =136,4 МПа.
- Найти напряжения возникающие в поперечном сечении стального стержня l=200 мм, если при нагружении растягивающим усилием его длина стала l1=200,1 мм. Принять МПа.
1) 10 МПа;
2) 100 МПа;
3) 50 МПа;
4) 120 МПа.
- Для заданного бруса определить наибольшие нормальные напряжения. Если F =10 кН, A=2 см2
1) 10 МПа;
2) 100 МПа;
3) 50 МПа;
4) 120 МПа.
- Определить изменение длины бруса. Если F=10 кН, A=2 см2, МПа, l=0,2 м
1) 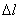= –0,15 мм;
2) 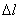= –2 мм;
3) 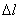= –3 мм;
4) 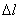= 4,5 мм.
- Две проволоки, одна стальная, другая медная, имеют одинаковую длину и нагружены одинаковыми растягивающими усилиями. Медная проволока имеет диаметр D=1 мм. Чему равен диаметр стальной проволоки, если обе проволоки удлиняются на одинаковую величину. Принять 
МПа, 
МПа
1) D
0,9 мм;
2) D0,71 мм;
3) D1,9 мм;
4) D0,98 мм.
- Стальной брус квадратного сечения под действие нагрузки удлиняется в продольном направлении на величину 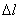=3,2·10–2 мм, а в поперечном направлении сжался на 
=0,03·10–2 мм. Найти коэффициент Пуассона 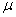, если l=30 см; h=1 см
1) 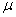=0,28;
2) 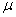=0,25;
3) 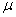=0,3;
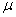4) =0,2.
- Стержень растягивается силой F = 15,7 кН, диаметр поперечного сечения D = 20 мм. Чему равны напряжения в поперечном сечении бруса?
1) 110 МПа;
2) 100 МПа;
3) 50 МПа;
4) 150 МПа.
- Проволока длиной l=10 м под действием растягивающей силы F=800 Н удлинилась на 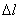=15 мм. Определить модуль упругости Е, если A=4 мм2.
1) МПа;
2) МПа;
3) МПа.
- Определить напряжение в канате, состоящем 36 проволок, каждая диаметром D=1 мм, при растяжении нагрузкой F=9 кН
1) =300 МПа;
2) =159,2 МПа;
3) =319 МПа;
4) =36,4 МПа.
- Стальной образец диаметром D=20 мм и расчётной длиной l=200 мм растянут на испытательной машине. Длина деформированного образца l1=200,15 мм. Определить растягивающее усилие, приняв модуль МПа.
1) N=47,1кН;
2) N=36,2 кН;
3) N=38 кН;
4) N=76,2 кН.
- Определить допускаемое значение нагрузки [F] для стального бруса, если A=10 см2, 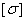=160 МПа.
1) [F] = 32 кН;
2) [F] = 68 кН;
3) [F] = 40 кН;
4) [F] = 48 кН.
- Для заданного бруса определить наибольшие нормальные напряжения и общее изменение длины бруса. Если F=10 кН, A=2 см2, МПа, l=0,2 м.
1) =10 МПа; 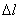= 1,6 мм;
2) = 80 МПа; 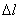= 2,2 мм ;
3) = 80 МПа; 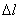= 0,16 мм;
4) = 40 МПа; 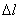= 4,5 мм.
- При подвешивании некоторого груза к стальной проволоке (МПа) длиной 3 м и диаметром 1,6 мм её удлинение оказалось равным 1,5 мм. Затем тот же груз был подвешен к медной проволоке длиной 1,8 м с диаметром 3,2 мм, и в этом случае удлинение получилось равным 0,39 мм. Определить модуль упругости медной проволоки.
1) МПа;
2) 
МПа;
3) МПа.
- Чугунная колонна (МПа) кольцевого поперечного сечения имеет наружный диаметр 30 см и толщину стенки 30 мм. Определить относительное укорочение колонны при нагрузке 600 кН, если высота колонны 4 м.
1) 
;
2) 
;
3) 
;
4) 
.
- Если F = 30 кН, А1 = 5 см2 , l = 0,5 м, Е = 200 ГПа, то удлинение стержня 1 (в мм) составит
1) 0,1
2) 0,2
3) 0,3
4) 0,5
- Если F = 250 кН, А = 25 см2 , l = 0,5 м, Е = 200 ГПа, а = 0,4 м, то изменение длины среднего участка (в мм) составит
1) 0,2
2) 0,3
3) 0,4
4) 0,5
- Стержни кронштейна, изготовленные из одного материала с коэффициентом линейного расширения 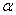нагреваются на 
градусов. При этом вертикальное перемещение узла В составит, полагая 
.
1) 
2) 
3) 
4) 
- Ступенчатый брус при нагружении заданными силами укоротится на величину, кратную 
1)
2)
3) 
4) 
- Наибольшее напряжение в конструкции равно, полагая
1) 
2) 
3) 
4) 
- Считая перемещение влево положительным и полагая , определите перемещение сечения В
1) 
2) 
3) 
4)
- Если предел текучести материала стержней равен 
, то при нагружении заданной силой F запас прочности конструкции равен, полагая 
1) 
2) 
3) 
4) 
- При нагружении бруса заданными силами наибольшее по модулю напряжение (в МПа) равно
1) 250
2) 220
3) 200
4) 160
- Наибольшее по модулю напряжение в брусе равно, полагая
1)
2) 
3)
4) 
- Тензометр Т, прикрепленный вдоль оси стержня 1, показывает деформацию 
= 4·10-4 . Чему равна величина силы F (в кН), если площадь поперечного сечения стержня А = 10 см2 ,и модуль Юнга Е= 200 ГПа?
1) 60
2) 70
3) 80
4) 90
- Если F = 320 кН, А = 40 см2 , = 240 МПа, то запас прочности бруса по пределу текучести равен
1) 1,5
2) 1,6
3) 2,0
4) 3,0
- Если А1 = 10 см2 , А2 = 16 см2 , [] = 160 МПа, то грузоподъемность кронштейна G (в кН) равна
1) 160
2) 172
3) 181
4) 190
- Если F = 200 кН, 
= 200 МПа, А1 = 16 см2 , 
= 340 МПа, А2 = 10 см2, то фактический запас прочности конструкции равен
1) 1,5
2) 1,6
3) 1,7
4) 1,8
- При нагружении заданной стержневой системы силой F отношение 
удлинений стержней 1 и 2 численно равно
1) 2,0
2) 
3) 0,5
4) 
- Деформация, замеренная тензометром Т, равна 
= 1,5 ·10-4 . Какова величина силы F (в кН), если ЕА = 200 МН?
1) 60
2) 80
3) 100
4) 120
- Считая известными размеры а, l, 
, площадь поперечного сечения A и модуль Юнга Е, определите монтажное усилие в стержне 2 после сборки системы, полагая 
1) 
2) 
3) 
4) 
- Для разгрузки вертикального стержня 1 дополнительно установлены стержни 2. Если все три стержня абсолютно одинаковы, то за счет установки наклонных стержней 2 разгрузка стержня 1 (в процентах) составит
1) 23
2) 28
3) 33
4) 43
- Жесткий брус ВД подвешивается на трех титановых стержнях, каждый из которых короче проектной длины на 0,1%. Если Е = 100 ГПа, то после сборки системы наибольшее монтажное напряжение составит (в МПа)
1) 20
2) 40
3) 60
4) 80
- Заделанный по концам брус подвергается температурному воздействию: часть АС нагревается, а часть СВ охлаждается на градусов. Определите напряжение в брусе, полагая 
1) 
2)
3) 
4) 
- Система состоит из трех одинаковых стальных стержней (Е = 200 ГПа, 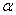= 12,5·10-6). На сколько градусов нужно нагреть всю систему, чтобы наибольшее напряжение достигло величины 100 МПа?
1) 40°
2) 50°
3) 60°
4) 80°
- При нагреве стержня 3 на градусов во всех стержнях системы возникли усилия. Какой температурный режим нужно создать для стержня 1, чтобы эти усилия исчезли?
1) охладить на
2) нагреть на
- Определите наибольшее по модулю напряжение в системе, полагая
1) 
2) 
3)
4)
- Если все стержни системы нагреть на одно и то же число градусов, то при задан942-75.gif">
- Для разгрузки стержня 1 вводится дополнительный стержень 2 (показан пунктиром), совершенно аналогичный стержню 1. В результате напряжение в стержне 1 уменьшится на величину (в процентах)
1) 15
2) 20
3) 25
4) 30
- На сколько градусов можно нагреть жестко защемленный по концам медный стержень, не нарушая его прочности, если Е = 100 ГПа, 
= 16·10-6, [
] = 80 МПа
1) 30
2) 40
3) 50
4) 60
- При нагружении системы силой F относительная деформация стержня 1, замеренная тензометром, составила величину 
= 5·10-4. Если А = 15 см2, Е = 200 ГПа, то величина силы равна (в кН)
1) 100
2) 200
3) 300
4) 400
