Логические операции

Высказывания и высказывательные формы

Элементы математической логики

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.

Примеры алгебр: алгебра натуральных чисел, алгебра рациональных чисел, алгебра многочленов, алгебра векторов, алгебра матриц, алгебра множеств и т. д.

Объектами алгебры логики, или булевой алгебры, являются высказывания.

Высказывание — это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное.

Всякое высказывание или истинно, или ложно; быть одновременно и тем и другим оно не может.

Формулировка любой теоремы является высказыванием. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков.

Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства. Сами числовые выражения высказываниями не являются. Например, предложение Х < 12 становится высказыванием при замене переменной каким-либо конкретным значением. Такие предложения называют высказывательными формами.

Примеры высказываний:

1) {Город Вашингтон — столица США} (истинное высказывание);

2) {Число 2 является делителем числа 7} (ложное высказывание);

3) {3 + 5 = 2 × 4} (истинное высказывание);

4) {2 + б > 10} (ложное высказывание);

5) {II + VI > VIII} (ложное высказывание);

6) {Сумма чисел 2 и 6 больше числа 8} (ложное высказывание);

7) {Two plus six is eight} (истинное высказывание);

8) {Na — металл} (истинное высказывание).

Высказывание называетсяпростым(элементарным), если никакая его часть сама не является высказыванием. Если это условие не выполняется, высказывание называетсясложным.

Высказывания, приведенные выше, являются простыми. Они обозначаются заглавными латинскими буквами:

А = {Аристотель — основоположник логики}.

В = {На яблонях растут бананы}.

Читать приведенные записи нужно так:

 

А есть высказывание «Аристотель — основоположник логики».

В есть высказывание «На яблонях растут бананы».

 

Обоснование истинности или ложности простых высказываний решается вне алгебры логики.

Например, истинность или ложность высказывания «Сумма углов треугольника равна 180 градусам» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Истинному высказыванию ставится в соответствие 1, ложному — 0.

Таким образом, А = 1, В = 0.

 

 

Будем считать, что уже имеется некоторый запас элементарных высказываний, относительно каждого из которых известно, истинно оно или ложно. В обычной речи мы часто используем слова, называемые логическими связками, — «не», «и», «или», «следует», «влечет», «эквивалентно», «равносильно», «тогда и только тогда, когда...» и т. п.

Примеры сложных высказываний:

1) {В автобусе можно доехать до школы и почитать журнал};

2) {Число 376 четно или двузначно};

3) {Неверно, что Солнце движется вокруг Земли};

4) {Если сумма цифр числа делится на 3, то число делится на 3}.

В алгебре логики, как и в обычной алгебре, вводится ряд операций. Рассмотрим пять основных логических операций.

1. Логическая операцияконъюнкция (лат. conjunctio — «связываю»):

• в естественном языке соответствует союзами,а,но,хотя;

• обозначение: & или Ù;

• иное название:логическое умножение.

Конъюнкция— это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Это определение распространяется и на случай п высказываний (п > 2, п —целое число). В соответствии с определением правила выполнения действий для операции конъюнкции можно представить в виде истинностной таблицы:

A	B	AÙB

Истина будет лишь в том случае, когда оба человека не лгут.

2. Логическая операциядизъюнкция (лат. disjunctio — «различаю»):

• в естественном языке соответствует союзуили;

• обозначение;

• иное название:логическое сложение.

Дизъюнкция — это логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из двух образующих его высказываний истинно.

Правила действия для операции дизъюнкции можно представить в виде истинностной таблицы:

A	B	AÚB

Выбирая между истиной и ложью, мы останавливаемся на истине.

В отличие от рассмотренной выше операции дизъюнкции можно рассмотреть строгую дизъюнкцию (двойное «или»), которой в естественном языке соответствует связка «либо..., либо...»). Суть этой операции ясна из приведенной ниже таблицы:

A	B	AÅB

Данная операция реализует сложение разряда двоичного числа без переноса в старший разряд.

3. Логическая операция импликация (лат. implicatio — «тесно связываю»):

• в естественном языке соответствует оборотуесли..., то...;

• обозначение: =>;

• иное название:логическое следование.

Импликация — это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Таблица истинности импликации:

A	B	AÞB

Из лжи может следовать что угодно, даже истина, но из истины не может следовать ложь.

4. Логическая операция эквиваленция (лат. aequivalens — «равноценное»):

• в естественном языке соответствует оборотам речитогда и только тогда, в том и только в том случае;

• обозначение:Û;

• иное название:равнозначность.

Эквиваленция — это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Эквивалентны ли высказывания, то есть одинаковы ли значения высказываний?

Таблица истинности эквиваленции:

A	B	AÛB

 

5. Логическая операция инверсия (лат. inversio — «переворачиваю»):

• в естественном языке соответствует словамневерно, что...и частицене;

• обозначение: ;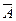

• иное название:отрицание.

Отрицание — это логическая операция, которая каждому данному высказыванию ставит в соответствие новое высказывание, которое истинно, если данное высказывание ложно, и ложно, если данное высказывание истинно.

Таблица истинности инверсии:

 

A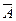

 

Логические операции имеют следующий приоритет: действия в скобках, отрицание, Ù, v, =>,<=>.