Адиабатический процесс. Уравнение адиабаты.
Адиабатический процесс – это процесс, который происходит без обмена теплом с окружающей средой, т.е.  .
.
Экспериментально адиабатический процесс можно осуществить следующими способами:
1. Быстрый процесс, когда система не успевает обменяться теплом с окружающей средой.
 2. С использованием сосуда Дьюара (термоса):
2. С использованием сосуда Дьюара (термоса):
3. Тело поддерживает одинаковую температуру со стенками сосуда.

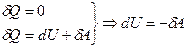
Т.е. изменение энергии происходит за счёт работы внешних сил.

Берём полный дифференциал:
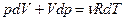 - здесь изменились ВСЕ параметры системы
- здесь изменились ВСЕ параметры системы

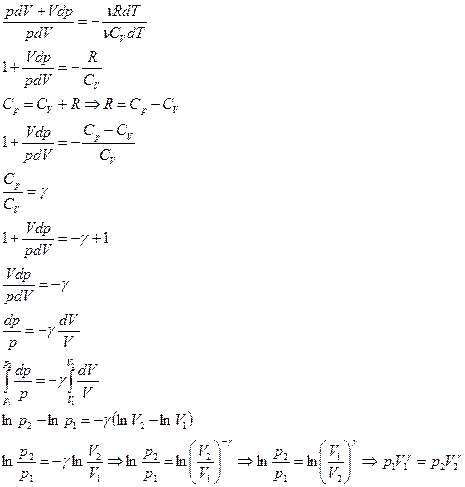
Т.к. состояния 1 и 2 выбраны произвольно, то получается, что
 - уравнение адиабаты
- уравнение адиабаты

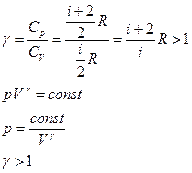
Для 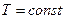
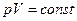

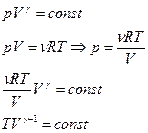
6. Работа, теплота и внутренняя энергия при изопроцессах и адиабатическом процессе.
Изохорный процесс ( ).
).

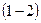 изохорное нагревание
изохорное нагревание
 изохорное охлаждение
изохорное охлаждение
При изохорном процессе газ не совершает работы над внешними телами, т.е.:

Из первого начала термодинамики ( ) для изохорного процесса следует, что вся теплота, сообщаемая газу, идёт на увеличение его внутренней энергии:
) для изохорного процесса следует, что вся теплота, сообщаемая газу, идёт на увеличение его внутренней энергии:  . Из формулы
. Из формулы  получаем, что
получаем, что  . Тогда для произвольной массы газа получим, что:
. Тогда для произвольной массы газа получим, что:
 .
.
Изобарный процесс ( ).
).

Работа газа:
 .
.
Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то:  и
и  , откуда
, откуда  .
.
Тогда выражение для работы изобарного расширения примет вид:

Из этого выражения вытекает физический смысл молярной газовой постоянной: если  , то для 1 моля газа
, то для 1 моля газа  , т.е.
, т.е. 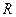 численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на
численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на  .
.
В изобарном процессе при сообщении газу массой  количества теплоты
количества теплоты

его внутренняя энергия возрастает на величину
 .
.
Изотермический процесс (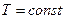 ).
).

Изотермический процесс описывается законом Бойля-Мариотта: 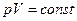 .
.
Диаграмма этого процесса в координатах  представляет собой гиперболу, расположенную тем выше, чем выше температура, при которой происходил процесс.
представляет собой гиперболу, расположенную тем выше, чем выше температура, при которой происходил процесс.
Исходя из выражения  и уравнения Менделеева-Клапейрона (
и уравнения Менделеева-Клапейрона ( ), работа изотермического расширения газа:
), работа изотермического расширения газа:
 .
.
Т.к. при 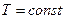 внутренняя энергия идеального газа не изменяется:
внутренняя энергия идеального газа не изменяется:
 ,
,
то из первого начала термодинамики следует, что:
 ,
,
т.е. всё количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
 .
.
Следовательно, для того, чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.