Безусловная оптимизация.
А
Методы для нахождения корня уравнения функции 1-ой переменной.
Деление пополам:
Имеется хотя бы 1 корень. Выбираем любую точку и смотрим какой знак она имеет, такой знак нам и искать. Выбираем точку приблизительно в середине интервала, исследуя значения в 3-х можно отбросить половину интервала.
 |
+
 |
b
-
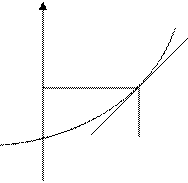
Метод Ньютона (метод касательной):
В случае если известна производная, то выбираем 
- начальное приближение.
 |
 |
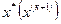
Допустим, что точка достаточно близка к корню функции и примерно себя ведет линейно не отклоняется. Проведем касательную и находим точку ближе чем , и повторяем до 
.
Для метода Ньютона необходимо:
- функция должна иметь производную;
- точка должна быть взята близко к корню;
- функция изменяется близко к линейной функции.
;
- уравнение касательной;
.
Если 
, то вычисления можно прекратить и считать что нужный нам корень – условие прекращения поиска. (Е – значение корня с некоторой точностью).
В методе Ньютона каждя его итерация удваивает количество значащих цифр. Если все условия выполнены, то эти методы удваивают (ускоряют) количество значащих цифр:
;
Представим что 
линейная функция, то метод Ньютона позволяет найти ее корень за 1-у итерацию. Целевая функция представляет собой квадратичную зависимость следовательно метод Ньютона позволяет найти минимум или максимум квадратичной функции за 1-у итерацию.
Замена функции на касательную, называется – линейная аппроксимация, и ее применение к целевой функции парабола в точке приближения.
 |
f(x)
 |
х
Замена заданной зависимости квадратичной зависимостью, называется – квадратичной аппроксимацией. Метод Ньютона основан на замене заданной зависимости более простой зависимостью.
Целевая функция зависит от нескольких переменных f(х1, х2, …, хn)® min. Т.к. нет дополнительных условий накладывающихся на переменные – безусловная оптимизация.