Основные характеристики алгоритма при его анализе. Вычислительная сложность алгоритма

Одну и ту же задачу может решать множество алгоритмов. Эффективность работы каждого из них описывается разнообразными характеристиками. Основные характеристики – это

· Вычислительная сложность;

· Запросы к памяти.

Прежде чем анализировать эффективность алгоритма, нужно доказать, что данный алгоритм правильно решает задачу. В противном случае вопрос об эффективности не имеет смысла.

При анализе алгоритма определяется количество «времени» для его выполнения. Это не реальное число секунд или других промежутков времени, а число операций, выполняемых алгоритмом. Число операций измеряет относительное время выполнения алгоритма или его вычислительную сложность. Фактическое количество секунд работы алгоритма непригодно для его анализа, т.к.

а) нас интересует относительная эффективность алгоритма;

б) алгоритм не становится лучше (хуже), если его перенести на более быстрый (медленный) компьютер.

Более того, даже фактическое количество операций алгоритма на тех или иных входных данных не представляет большого интереса и не очень много сообщает об алгоритме. Вместо этого более важной и интересной является зависимость числа операций алгоритма от размера входных данных. Мы можем сравнивать два алгоритма по скорости роста числа операций. Именно скорость роста играет ключевую роль, и, как правило, рассматривается как показатель вычислительной сложности алгоритма, поскольку при небольшом размере входных данных алгоритм А может требовать меньшего количества операций, чем алгоритм В, но при росте объема входных данных ситуация может поменяться на противоположную.

Два самых больших класса алгоритмов – это

алгоритмы с повторением,
рекурсивные.

В основе алгоритмов с повторением лежат циклы и условные выражения; для анализа таких алгоритмов требуется оценить число операций, выполняемых внутри цикла, и число повторений цикла.

Рекурсивные алгоритмы разбивают большую задачу на фрагменты и применяются к каждому фрагменту отдельно. Такие алгоритмы называются иногда «разделяй и властвуй». В процессе решения большой задачи путем деления ее на меньшие создаются небольшие простые и понятные алгоритмы. Анализ рекурсивного алгоритма требует подсчета количества операций, необходимых для разбиения задачи на части, выполнения алгоритма на каждой из частей и объединения отдельных результатов для решения задачи в целом. Объединяя эту информацию и информацию о числе частей, мы можем вывести рекурентное соотношение для сложности алгоритма.

Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Для каждого алгоритма необходимо оценивать, насколько быстро решается задача на множестве (массиве) входных данных длины .

Одну и ту же задачу часто можно решить при помощи различных алгоритмов. Анализ алгоритмов дает инструмент для выбора алгоритма.

Пример. Выбрать наибольшую из трех величин .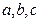

В каждом алгоритме делается два сравнения. Первый алгоритм легче прочесть и понять, но с точки зрения выполнения на компьютере у них одинаковый уровень сложности, но первый требует больше памяти из-за временной переменной . Это не играет значительной роли, если сравниваются числа или символы, но при работе с другими типами данных это может стать существенным. Многие современные языки программирования позволяют определять операторы сравнения для больших и сложных объектов или записей. В этих случаях размещение временной переменной может потребовать много места. При анализе эффективности алгоритмов нас, в первую очередь, будет интересовать вопрос времени, но в тех случаях, когда память играет существенную роль, мы будем обсуждать и ее.

Различные характеристики алгоритмов предназначены для сравнения эффективности разных алгоритмов, решающих одну задачу. Не имеет смысла сравнивать между собой, например, алгоритм сортировки и алгоритм умножения матриц.

Результат анализа алгоритмов – не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Такая информация бесполезна, т.к. в этом случае нужно указывать также тип компьютера, используется ли он одним пользователем или несколькими, какой у него процессор и тактовая частота, полный или редуцированный набор команд на чипе процессора и насколько хорошо компилятор оптимизирует выполняемый код. Эти условия влияют на скорость работы программы, реализующей алгоритм. Учет этих условий означал бы, что при переносе программы на более быстрый компьютер алгоритм становится лучше, т.к. он работает быстрее. Но это не так, поэтому анализ не должен учитывать указанных особенностей компьютера.

В случае небольшой или простой программы количество выполняемых алгоритмом операций как функцию от можно посчитать точно. Однако в большинстве случаев в этом нет нужды. Действительно, рассмотрим для примера два простых гипотетических алгоритма, один из которых требует для своей реализации 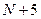операций, а второй - . Очевидно, что разница между ними становится незаметной, как только становится достаточно большим. В силу этого имеет смысл оценивать главный член в формуле зависимости количества операций от размера входных данных. В рассмотренном случае - это .

2. Классы входных данных

Роль входных данных в анализе алгоритмов чрезвычайно велика, поскольку последовательность действий алгоритма определяется не в последнюю очередь входными данными. Например, чтобы найти наибольший элемент в списке из 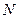элементов, можно воспользоваться следующим алгоритмом:

Если список изначально упорядочен в порядке убывания, то перед началом цикла будет сделано одно присваивание, а в теле цикла присваиваний не будет вообще. Если список первоначально упорядочен по возрастанию, то всего будет сделано 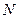присваиваний. При анализе необходимо рассмотреть различные возможные множества входных данных, поскольку при ограничении одним множеством, оно может оказаться тем самым, на котором решение самое быстрое (медленное). В результате можно получить ложное представление об алгоритме. Вместо этого, как правило, рассматриваются все типы входных множеств. Для этого различные входные множества разбиваются на классы в зависимости от поведения алгоритма на каждом множестве. Такое разбиение позволяет уменьшить количество рассматриваемых возможностей. Например, число различных расстановок 10 различных чисел в списке есть 10!=3628800. Применим к списку из 10 чисел алгоритм поиска наибольшего элемента. Имеется 362880 входных множеств, у которых первое число является наибольшим; они все помещаются в один класс. Для любого множества из этого класса алгоритм сделает единственное присваивание. Если наибольшее по величине число стоит на втором месте, то алгоритм сделает ровно два присваивания. Все такие множества (их 362880) можно поместить в другой класс. Очевидно, число присваиваний будет на единицу возрастать при последовательном изменении положения наибольшего числа от 1 до 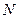. Таким образом можно разбить все входные множества на 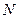разных классов по числу производимых присваиваний. Очевидно, нет необходимости выписывать или описывать детально все множества, оказавшиеся в одном классе.

Как только выделены классы, просматривается поведение алгоритма на одном множестве из каждого класса. Если классы выбраны правильно, то на всех множествах входных данных одного класса алгоритм производит одинаковое количество операций, а на множествах из другого класса это количество, в общем случае, будет другим.