Расчеты на прочность и жесткость при растяжении (сжатии)

Рис. 2.12

Рис. 2.11

Рис. 2.10

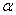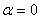Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, проходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла . При из (2.21) следует, что 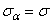, 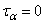. При 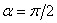, т.е. на продольных площадках, 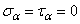. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения принимают наибольшие значения при 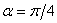, и их величина составляет 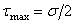. Важно отметить, что 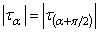. Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряжения равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название закона парности касательных напряжений.

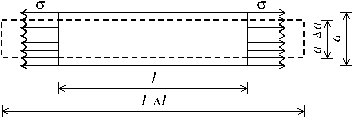
Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направлении сопровождается пропорциональным уменьшением поперечных размеров стержня (рис. 2.11).

Если обозначить:

; ; ,

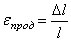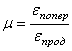то, как показывают эксперименты, 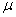= const для данного материала и является безразмерным коэффициентом Пуассона. Величина 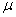является важной характеристикой материала и определяется экспериментально. Для реальных материалов 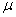принимает значения 0,1...0,45.

При растяжении стержня возникают не только линейные, но и угловые деформации.

Рассмотрим прямой угол АВС (рис. 2.12, а), образованный отрезками АВ и АС, в недеформированном состоянии.

При растяжении стержня точки А, В и С займут положение А¢, B¢, C¢ соответственно. Величина

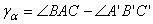
называется угловой деформацией или угловым сдвигом в точке А.

Совместим точки А и А¢ и рассмотрим взаимное расположение отрезков АВ и А¢B¢(рис. 2.12, б). На этом рисунке отметим вспомогательные точки K и L и прямую n, перпендикулярную отрезку А¢B¢. Из рис. 2.12, б имеем:

; ,

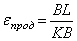откуда с учетом 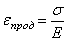получим:

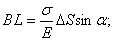
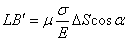. (2.22)

Для определения спроектируем ломаную 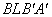на ось n

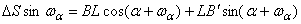откуда, учитывая малость угла , т.е. , , 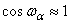получим:

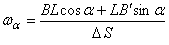. (2.23)

В результате совместного рассмотрения (2.22) и (2.23) получим:

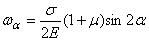Откуда .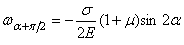

Следовательно, 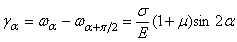. (2.24)

Сопоставляя выражение 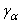с выражением 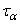из (2.21) окончательно получим закон Гука для сдвига:

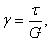(2.25)

где величина 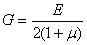называется модулем сдвига или модулем упругости материала второго рода.

Основной задачей расчета конструкции является обеспечение ее безопасной эксплуатации. Важнейшим условием, обеспечивающим безопасную эксплуатацию конструкции, является условие прочности. Существуют различные методы обеспечения прочности конструкций. Мы чаще всего будем пользоваться одним из этих методов – расчетом по допускаемым напряжениям. Согласно этому методу для конструкций, работающих на растяжение-сжатие, условие прочности, составленное для опасного сечения, можно записать в таком виде:

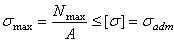(2.26)

где – максимальное напряжение в конструкции; 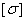– характеристика материала, называемая допускаемым напряжением.

Допускаемое напряжение находится по формуле

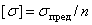. (2.27)

где 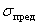– предельное напряжение, при достижении которого в стержне наступает предельное состояние материала: появляются пластические деформации, если материал стержня – пластичный, или происходит разрушение, если стержень выполнен из хрупкого материала; n – нормируемый коэффициент запаса прочности.

Кроме формулы (2.26), возможен второй вариант условия прочности

, (2.28)

где 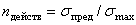(2.29)

называется действительным коэффициентом запаса прочности, показывающим во сколько раз надо увеличить максимальное напряжение в стержне, чтобы материал стержня оказался в опасном (предельном) состоянии.

Условие прочности в зависимости от цели поставленной задачи позволяет выполнять расчеты на прочность двух видов: проектный и проверочный. Для спроектированного стержня можно также определять допускаемую нагрузку.

Проектный расчет выполняют с целью определения размеров поперечных сечений элемента конструкции при известных рабочих нагрузках и материале (допускаемых напряжений). Площадь поперечного сечения определяют из выражения

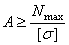. (2.30)

Форма сечения стержня не влияет на его прочность при растяжении (сжатии). Форму сечения стержня необходимо знать только для определения размеров сечения при известном значении площади.

Зная площадь сечения и его форму, находят размеры сечения.

Проверочный расчет выполняют для спроектированной конструкции с целью проверки ее прочности. При проверочном расчете должны быть известны площадь опасного сечения, нагрузка и материал (допускаемое напряжение). Проверочный расчет выполняют по формуле (2.26).

Определение допускаемой нагрузки для спроектированного элемента конструкции, размеры поперечного сечения которого и материал (допускаемые напряжения) известны. Условие прочности в этом случае записывают в виде

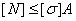. (2.31)

Зная значение 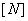, определяют допускаемую нагрузку .

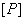Так как допускаемые напряжения не имеют точного значения, а выбираются приближенно, то при проверочном расчете максимальные рабочие напряжения могут превышать допускаемые на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки так, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки та, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%.

При проектировании элементов конструкций стремятся сделать их во всех сечениях равнопрочными.

Рассмотренные три вида расчетов на прочность можно выполнять не только при растяжении или сжатии, а при любом виде деформации (сдвиге, кручении, изгибе).

При проектировании строительных конструкций расчет на прочность стальных элементов, подверженных центральному растяжению или сжатию, следует выполнять по формуле

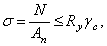(2.32)

где 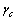– коэффициент условий работы, принимаемый по СНИП (см. табл.2.1) или другим нормам.

Таблица 2.1

Элементы конструкции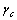

Колонны общественных зданий и опор водонапорных башен Элементы стержневых конструкций покрытий и перекрытий: а) сжатых при расчетах на устойчивость б) растянутых в сварных конструкциях Сплошные составные балки, колонны, несущие статическую нагрузку и выполненные с помощью болтовых соединений, при расчетах на прочность Сечения прокатных и сварных элементов, несущих статическую нагрузку, при расчетах на прочность Сжатые элементы из одиночных уголков, прикрепляемые одной полкой

0,95 0,95 0,95 1,1 1,1 0,75

Примечание: В случаях, не оговоренных в настоящих нормах, в формулах следует

принимать .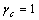

Для хрупких строительных материалов условия прочности принимают вид:

при растяжении: , ;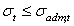

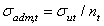при сжатии: 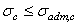, 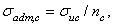(2.33)

где 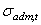и 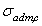– допускаемые напряжения при растяжении и сжатии; n_t и n_c – нормативные коэффициенты запаса прочности по отношению к пределу прочности (n_t, n_c>1).

Для центрально сжатых бетонных элементов формула (2.33) записывается в виде:

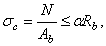(2.34)

где 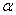– коэффициент, принимаемый для бетона тяжелого, мелкозернистого и легкого равным 1,00; для ячеистого автоклавного – 0,85; для ячеистого неавтоклавного – 0,75.

В некоторых случаях работоспособность элемента конструкции определяется не только его прочностью, но и жесткостью, т.е. способностью элемента воспринимать нагрузки без недопустимых упругих деформаций. При расчетах на жесткость определяют максимальные перемещения сечений и сопоставляют их с допускаемыми перемещениями.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:

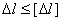где 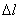- изменение размеров детали;

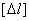- допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин 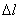по участкам

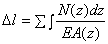, (2.35)

условие жесткости при растяжении (сжатии) запишем следующим образом:

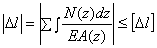. (2.36)

Так как перемещение, согласно закону Гука, зависит от нагрузки и размеров поперечного сечения, условие жесткости позволяет решать те же три вида задач, что и условие прочности.