Напряженное и деформированное состояние при растяжении и сжатии
Рис.2.9
вторым слагаемым, в силу его малости, можно пренебречь, и тогда
 . (2.14)
. (2.14)
Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении 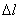 будет равна площади треугольника ОСВ (рис. 2.9), т.е.
будет равна площади треугольника ОСВ (рис. 2.9), т.е.
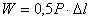 . (2.15)
. (2.15)
В свою очередь, когда напряжения  и деформации
и деформации  распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:
распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:
 . (2.16)
. (2.16)
Поскольку, в данном случае имеем, что 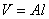 ,
,  и
и 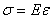 , то
, то
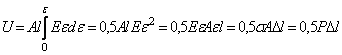 , (2.17)
, (2.17)
т.е. подтверждена справедливость (2.12).
С учетом (2.8) для однородного стержня с постоянным поперечным сечением и при Р = const из (2.17) получим:
 . (2.18)
. (2.18)
Единицей измерения потенциальной энергии деформации является 1Hм = 1Дж.
Рассмотрим более подробно особенности напряженного состояния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, составляющей угол 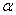 с плоскостью нормального сечения (рис. 2.10, а).
с плоскостью нормального сечения (рис. 2.10, а).
Из условия 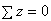 , записанного для отсеченной части стержня (рис. 2.10, б), получим:
, записанного для отсеченной части стержня (рис. 2.10, б), получим:
 , (2.19)
, (2.19)
где A - площадь поперечного сечения стержня,  - площадь наклонного сечения. Из (2.19) легко установить:
- площадь наклонного сечения. Из (2.19) легко установить:
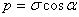 . (2.20)
. (2.20)
Раскладывая напряжение р по нормали и касательной к наклонной площадке (рис. 2.10, в), с учетом (2.20) получим:
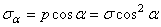 ;
; 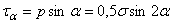 . (2.21)
. (2.21)
