Пример 1.

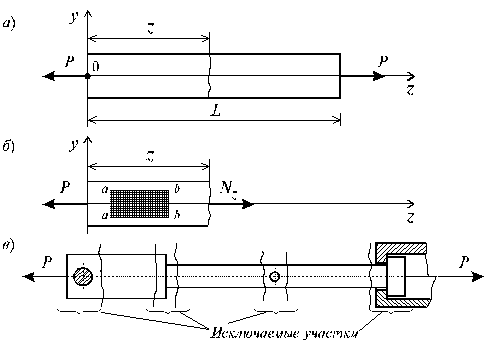
Рис. 2.2

Рис.2.1

 

Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось направим вдоль продольной оси стержня.

Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (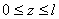) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:

,

откуда следует, что

.

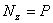Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения

(2.1)

 

Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Рассмотрим несколько примеров определения внутренних сил.

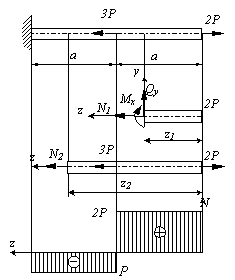
Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня, показанный на рис.2.3. Определить величину внутренних сил.