Двумерное волновое уравнение. Метод спуска

Контрольні питання

1. Какая геометрическая форма ячеек используется при проектировании сотовых систем?

2. В чем заключается принцип многократного использования частот в сотовых сетях?

3. Перечислите пять способов повышения пропускной способности сотовой сети.

4. Поясните, в чем состоит функция избирательного вызова сотовых систем?

5. Перечислите и кратко опишите различные наборы параметров, которые можно использовать для принятия решения о переключении.

6. Если во время связи с базовой станцией мобильное устройство перемещается, какие факторы определяют необходимость и степень регулирования мощности?

7. Объясните разницу между регулированием мощности по замкнутому и разомкнутому циклу.

8. Чем отличается интенсивность трафика от средней частоты вызовов в системе?

[1] Обычно выбранная антенна, а следовательно, и базовая станция, является ближайшей к мобильному устройству. Однако из-за аномалий в распространении сигнала это не всегда так.

[2] В американской документации стандартов сотовой сети используется термин handoff документации Международного телекоммуникационного союза (ITU) — термин handover. В технической литературе встречаются оба термина; поскольку они означают одно и то же, на русский язык их принято переводить одинаково — переключение.

Если начальные возмущения j и y не зависят от z, то, очевидно, и функция u, даваемая формулой (2.8.3), также не будет зависеть от переменного z. Следовательно, эта формула будет удовлетворять уравнению

(1)

и начальным условиям , .

Таким образом, формула, дающая решение пространственной задачи, позволяет также решить задачу для плоскости.

В формуле (2.8.3) интегрирование происходит по сфере . В силу независимости начальных данных от z интегрирование по верхней полусфере можно заменить интегрированием по кругу , получающемуся при пересечении сферы с плоскостью (рис. 5.). Элемент поверхности связан с элементом плоскости соотношением

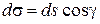
где

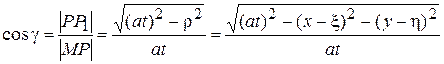угол между нормалью к плоскости и к сфере в точке P.

То же относится к интегрированию по нижней полусфере, следовательно, интеграл по кругу следует взять дважды.

В результате мы приходим к формуле

, (2)

в которой интегрирование производится по внутренности круга радиуса at с центром в точке . Здесь x и h - координаты точки P, - координаты точки M.

Аналогично, если j и y зависят только от одной переменной x, то мы получим решение Даламбера.

M y

P₁

Рис. 5

Физическая интерпретация. Пусть начальное возмущение задано в области на плоскости . Рассмотрим изменение состояния в точке , лежащей вне . Состояние в точке в момент t определяется согласно формуле (2) начальными значениями в точках P, принадлежащих кругу радиуса с центром в . Для моментов времени (d – расстояние от до ближайшей точки области ) функция = 0 – до точки возмущение еще не дошло. Если 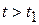, то . Это значит, что начиная с момента , в точке возникает возмущение, которое сначала, возрастает, а затем, начиная с некоторого момента, постепенно убывает до нуля (при ). В этом явлении последействия и заключается отличие плоского случая от пространственного. Влияние начальных возмущений, локализованных на плоскости, не локализовано во времени и характеризуется длительно продолжающимся последействием.

Мгновенная картина возмущений на плоскости имеет место резко очерченный передний фронт, но не имеет заднего фронта.

В заключение этого раздела рассмотрим примеры решения задачи Коши для уравнений в частных производных второго порядка.

Пример 1.Найти общее решение и решение задачи Коши уравнения в частных производных

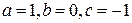Решение. Для того, чтобы найти общее решение методом Даламбера, преобразуем данное уравнение к каноническому виду. Вычислим дискриминант данного уравнения . Следовательно, данное уравнение гиперболического типа. Составим характеристическое уравнение . Учитывая то, что получим уравнение:

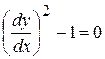или .

Откуда получим общие интегралы: . Введем, согласно общей теории преобразований, новые переменные

По формулам для частных производных найдем выражения в новых переменных:

Подставляя эти выражения в исходное уравнение, получим канонический вид в новых переменных:Решим полученное уравнение. Для этого введем обозначение . Тогда решаемое уравнение будет иметь следующий вид: . Решим его и найдем . Запишем полученное уравнение в виде . Откуда, интегрируя, получим и . Тогда учитывая введенное обозначение . Интегрируя по , получим общее решение в следующем виде: . Заменим новые переменные старыми: .

Найдем теперь решение задачи Коши. Согласно начальным условиям

. Откуда находим ,

Вычислим производную .

Тогда . Подставляя в это выражение найденное ранее выражение для производной , получим уравнение

Откуда . Следовательно, Подставляя в общее решение эти функции, получим решение задачи Коши: . Проверим найденное решение: вычислим частные производные . Подставляя вычисленные значения частных производных в исходное уравнение замечаем, что решение найдено верно. Начальные условия также выполняются: . То есть, задача Коши решена верно.

Пример 2.Найти общее решение и решение задачи Коши уравнения в частных производных

Решение. Сумма любых двух частных решений этого уравнения снова будет его решением. Поэтому, будем искать сначала частные решения методом разделения переменных: , . Подставляя первое выражение в исходное уравнение, получим или . Левая часть последнего уравнения является функцией , а правая – функцией . Поэтому это равенство возможно только в том случае, если и левая и правая части равны одной и той же константе. Следовательно, , . Решая эти уравнения, получим , . Тогда одним из частных решений исходного уравнения будет . Будем искать другое частное решение в виде . Подставляя в исходное уравнение, получим или . Левая часть последнего уравнения является функцией , а правая – функцией . Следовательно, эти функции равны одной и той же константе, то есть

, . Решим эти уравнения. Решение первого будем искать в виде . Подставляя в первое уравнение, получим . Откуда находим, что . Тогда . Решим второе уравнение. Интегрируя, получим . Откуда . Следовательно, вторым частным решением будет функция . Сумма частных решений также будет решением, то есть общее решение будет иметь следующий вид

где - произвольные константы интегрирования. Решим теперь задачу Коши. По условию задачи

Следовательно, . То есть, . Легко проверить, что второе условие задачи Коши также выполняется . Таким образом, решением задачи Коши является функция .