Агрегатная модель Бусленко

Агрегатная модель Бусленко. Дискретно-непрерывная система Глушкова. Гибридная система А.Пнуэли Модель индустриальной динамики Дж. Форрестера. Модели Мезаровича-Пестеля. Многоагентное моделирование. Когнитивные модели.

Макроэкономическое моделирование

Лекция 8

 

При системном подходе АСУ рассматривают как единую сложную систему совместно с управляющими подсистемами. Для обеспечения высокого качества управления необходимо хорошо знать свойства управляемых подсистем. Для того чтобы выявлять свойства управляемых подсистем, их реакцию на применяемые решения и мероприятия, а также оценивать качество принимаемых решений, необходимо использовать в работе АСУ результаты моделирования функционирования подсистем в тех или иных прогнозируемых условиях. Для решения этих задач можно применяют агрегатную модель Н.П.Бусленко. Агрегатная модель описывает объект управления в виде многоуровневой структуры из динамических систем заданных типов или агрегатов. При этом системы рассматриваются как обобщающий (самый общий и самый сложный) класс сложных систем и называются агрегативными. Агрегат используется для моделирования элементарных блоков сложных систем. Агрегативной системой называется любая совокупность агрегатов, если передача информации между ними происходит мгновенно и без искажений.

Агрегатом называется математическая модель вида:

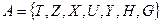, (8.1)

где

Т – интервал моделирования (обычно конечный);

Z – множество состояний (фазовое пространство);

X – множество входных сигналов;

U – множество управляющих (особенных) сигналов;

Y – множество выходных сигналов;

Н – оператор переходов, который определяет текущее состояние по предыстории;

G – оператор выходов.

В общем случае все последовательности событий в агрегате являются реализациями случайных последовательностей с заданными законами распределения, оператор Н также является случайным оператором.

Н.П. Бусленко при рассмотрении сложных систем выделяет два типа состояний:

1) обычные (неособые) состояния, в которых система находится почти все время;

2) особые состояния, характерные для системы в некоторые изолированные моменты времени, совпадающие с моментами получения входных и управляющих сигналов или выдачи выходного сигнала, в эти моменты состояние агрегата может измениться скачкообразно, а между особыми состояниями изменение координат происходит плавно и непрерывно.

Агрегат представляет собой математическую схему общего вида, частным случаем которой являются функции алгебры логики, релейно-контактные схемы, конечные автоматы, динамические системы, описываемые обыкновенными дифференциальными уравнениями и ряд других.

Модель агрегата может быть использована как модель всей непрерывно-дискретной системы или ее элемента. В этом случае система представляется сетью агрегатов с фиксированными каналами связей.

В качестве примера автоматизированной системы управления с разветвленной информационной частью и весьма сложными алгоритмами обработки информации можно рассмотреть систему управления полетом самолетов крупного аэродрома.