Доказательство

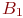Пусть равномощно подмножеству множества , а равномощно подмножеству множества .

Рис.

 

При взаимно однозначном соответствии между и подмножество переходит в некоторое подмножество . При этом все три множества , 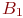и равномощны, - и нужно доказать, что они равномощны множеству , или, что то же самое, .

Теперь можно забыть про множество и его подмножества и доказывать такой факт:

если и равномощно , то все три множества равномощны.

(Для единообразия будем говорить вместо .)

Пусть - функция, осуществляющая взаимно однозначное соответствие (элемент соответствует элементу ). Когда переходит в , меньшее множество переходит в некоторое множество (см. рис. ниже)). Аналогичным образом само переходит в некоторое множество . При этом , так как .

Рис.

 

Продолжая эту конструкцию, получаем убывающую последовательность множеств

и взаимно однозначное соответствие , при котором соответствует (иногда это записывают так: ). Формально можно описать как множество тех элементов, которые получаются из какого-то элемента множества после -кратного применения функции . Аналогичным образом состоит из тех и только тех элементов, которые получаются из какого-либо элемента множества после -кратного применения функции .

Заметим, что пересечение всех множеств вполне может быть непусто: оно состоит из тех элементов, у которых можно сколько угодно раз брать - прообраз. Теперь можно сказать так: множество разбито на непересекающиеся слои и на сердцевину .

Слои , , , равномощны (функция осуществляет взаимно однозначное соответствие между и , между и и т.д.):

То же самое можно сказать про слои с нечетными номерами:

Можно отметить, что функция на множестве осуществляет его перестановку (взаимно однозначное соответствие с самим собой).

Построим взаимно однозначное соответствие между и . Пусть . Тогда соответствующий ему элемент строится так: при и при или (см. рис.)

Рис.

Теорема Кантора-Бернштейна значительно упрощает доказательства равномощности: например, если нужно доказать, что бублик и шар в пространстве равномощны, то достаточно заметить, что из бублика можно вырезать маленький шар (гомотетичный большому), а из шара - маленький бублик.

 

При сравнении мощностей для заданных множеств и теоретически имеются четыре возможности: