Метод дихотомии ( половинного деления.).

Если мы вычислим значения f в двух точках x₁,x₂ , то станет возможным исключение из рассмотрения некоторого множества точек, на котором гарантировано нет минимума, то есть имея измерения в двух точках можем сократить интервал поиска.

Как лучше выбирать точки, чтобы процесс быстрее сходился?

В методе дихотомии предлагается (отрезок [0,1] ).

Остается один из интервалов: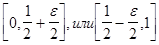. Выберем 3-й и 4-й эксперимент на e-пару в середине оставшегося интервала. После n (n-четно) экспериментов min функции лежит в интервале .

Здесь каждый раз два эксперимента, но можно один, а в качестве другого брать один из предыдущих.

 

 

3. Метод «золотого» сечения.

 

Интервал [a,b], вычислить функцию 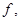в точках .

На интервале [a,b] расположен минимум функции.

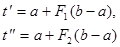, где F₁ и F₂ некоторые числа 0<F₁<1, 0<F₂<1.

 

Анализируем перегибы функции внутри интервала, и также, как раньше, заменяем отрезок [a,b] на 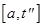или 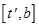. Идея метода в том чтобы после замены, необходимо было вычислить только одну точку при гарантированном уменьшении длины отрезка, т.е.

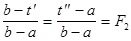Þ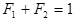, так как

(после замены отрезок уменьшится в 1/ F₂ = t

В новом отрезке должно быть(по правилу «золотого» сечения): так как

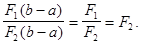
Тогда так как 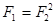, , 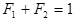то.

Таким образом, уменьшение интервала в 1/ F₂ = t раз достигается с помощью вычисления функции в одной новой точке (см. процедуру выполнения). После n экспериментов имеем интервал неопределенности:

.

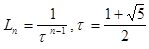В пересчете на одно измерение этот метод лучше дихотомии.

Процедура выполнения:

Рассмотрим [a,b], вычислить функцию 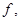в точках .

1)

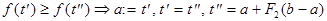
2)

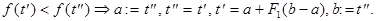
В 1) и 2) появилась только одна новая точка. И так далее, пока длина отрезка [a,b] не станет меньше заданной величины.