Метод квадратичной интерполяции.

Методы прямого поиска в задачах одномерной минимизации.

Литература к лекциям 2-3.

1.М.А. Королев, Т.Ю. Крупкина, М.А. Ревелева. Технология, конструкции и методы моделирования кремниевых интегральных микросхем. Часть 1. М.: БИНОМ. Лаборатория знаний. 2007. 397с.

Дополнительная литература

Черняев В.Н. Технология производства интегральных микросхем и микропроцессоров.М.: Радио и связь, 1987.

2. Броудай И., Мерей Д. Физические основы микротехнологии. - М.: Мир, 1985.

4. Ефимов И.Е., Козырь И.Я., Горбунов Ю.И. Микроэлектроника. Физические и технологические основы, надежность: Учеб. пособие для прибостроит. спец. вузов / М.; Высш. шк., 1986 г.

5. Коледов Л.А. Технология и конструкции микросхем, микропрорцессоров и микросборок: Учебник для вузов / М.: Радио и связь, 1989 г

min-?

x_k+1 = x_k + t_kS_k , где S_k -направление.

Необходимо определить t_k.

g(t) = f(x_k + tS_k)- найти минимум функции одной переменной (нет анализа заданной функции). Будем искать точку локального минимума, поэтому ограничимся функциями, имеющими один минимум. Больше ничего о функции неизвестно. Можно вычислить (измерить) значения функции в точках.

Пусть функция задана на прямой, даны при этом точки a<b<c, и 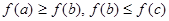, точка минимума в [a, c]

Через эти точки проведем параболу:

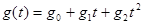
Положим:

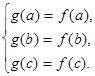, т.е. имеем 3 уравнения и 3 неизвестных g₀, g₁, g₂.

Находим g₀, g₁, g₂

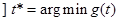
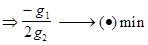
Рассмотрим два случая:

1)

2)

Так поступаем до тех пор, пока точка 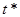не окажется в достаточно малой окрестности одной из трех точек a, b, c. После чего такую точку считаем точкой минимума.

Метод можно обобщить на случай кубических и т.д. функций, но потребуется вычислять большее количество точек.