Без доказательства

Доказательство

Cвойства выпуклых функций

Определение

Определение

Функция f(x), для которой -f(x) выпукла называется вогнутой.

Функция f(x) на R_n называется строго выпуклой, если "x¹y, 0<l<1 выполняется

f(lx+(1-l)y)<lf(x)+(1-l)f(y),

сильно выпуклой с константой l>0, если при 0£ l £1 выполняется

f(lx+(1-l)y)£lf(x)+(1-l)f(y)-ll(1-l)||x-y||²/2

1.Теорема:

Любая точка локального min выпуклой функции является в то же время точкой глобального минимума.

· Под интегралом:

(Ñf(x_k-ttÑf(x_k))-Ñf(x_k),-tÑf(x_k))£

Из условия теоремы известно:

||Ñf(x)-Ñf(y)||£ L||x-y||

В данном случае:

x-y = -ttÑf(x_k), то есть ||Ñf(x_k-ttÑf(x_k))-Ñf(x_k)||£ L||- ttÑf(x_k)||

и тогда соответствующее скалярное произведение:

£ L(- ttÑf(x_k), - tÑf(x_k)) = Lt²t||Ñf(x_k)||²

Пусть x*- точка локального минимума функции, она не является точкой глобального минимума, то есть $yÎX такая что:

f(y)<f(x*) (*)

Рассмотрим точки вида x = ly+(1-l)x* ,lÎ(0,1)

Так как X выпукло, то xÎX (по определению). Из выпуклости функции f(x)

и из (*)следует:

f(x)=f(ly+(1-l)x*)£(по вып.)lf(y)+(1-l)f(x*)<(*)lf(x*)+(1-l)f(x*)=f(x*)

Получено: f(x)<f(x*) "l

Но это противоречит условию, говоря о том, что х*- локальный минимум, так как при малых l точка х находится в достаточно малой окрестности точки х*.

Тогда теорема доказана от противного.

Теорема(о сильно выпуклой функции)

Сильно выпуклая функция обязательно имеет точку локального минимума, которая совпадает с точкой глобального минимума.

2.Теорема:

Пусть функция f (х) имеет вторую непрерывную производную. Для того,

чтобы функция была выпуклой необходимо и достаточно, чтобы ее вторая

производная была неотрицательна.

Без доказательства

Для сильно выпуклых функций: Ѳf (x) ³ l_*I., где I- единичная матрица, l>0

Эту теорему можно рассматривать как критерий выпуклости

дифференцируемых функций.

 

Замечание:

Не все выпуклые функции дифференцируемы.

Примеры:

1.f(x) = ïxï-выпуклая, не дифференцируемая

2.y = x² выпуклые, проверка выпуклости

y = -ln(x) по второй производной

 

3.Теорема (неравенство Йенсена):

Чтобы фукция f (x) была выпукла необходимо и достаточно, чтобы

" m ³2, x₁,x_2,…,x_mÎХ и l_i ³ 0 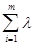_i =1 выполнялось:

_{m m}

f ( å l_i* x_i ) £ å l_{i *} f (x_i ). (*)

^{i=1 i=1}

Доказательство:

1. Достаточность, т.е. справедлива (*), нужно доказать выпуклость: пусть

m = 2, тогда f (x) – выпукла по определению.

2. Необходимость, т.е. дана выпуклость, нужно доказать (*): при m = 2 (*)

выполняется по определению.

3.Пусть при m = k теорема доказана (индукционное предположение).

Докажем при m = k + 1:

l_k+1¹1, тогда 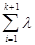_i x_i = l_k+1*x_k+1 + (1 - l_k+1)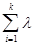_{* i *} x_i /(1 - l_k+1),

тогда 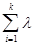_{i *} x_i ÎХ., так как выпуклое множество содержит все выпуклые

комбинации своих множеств.

Воспользуемся свойством выпуклости функций:

f (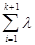_i* x_i ) £ l_k+1*f (x_k+1) + (1 - l_k+1)_* f ( 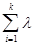_i* x_i/(1 - l_k+1)) £

Предположим, что теорема доказана для m=k

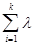_i/(1-l_k+1)= (1-l_k+1)/ (1-l_k+1)=1 удовлетворяет условиям теоремы (сумма всех коэффициентов равна 1)

£ l_k+1*f (x_k+1) + (1 - l_k+1)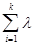_{* i *} f (x_i)/(1 - l_k+1) = 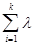_{i *} f (x_i )

Неравенство доказано.

 

4.Теорема:

Выпуклая функция f (x) , определенная на выпуклом множестве X непрерывна в

каждой внутренней точке этого множества и имеет в каждой внутренней точке

производную в любом направлении.