Доказательство
Градиентный метод с постоянным шагом
Методы первого порядка (градиентные методы)
Для вычисления t и S используются значение функции и первая производная.
Известно, что градиент функции в точке дает направление наибольшего возрастания функции в точке. Направление наибольшего убывания - это направление антиградиента.
Пусть Sk = -Ñf(xk), tk-длина шага.
Пусть tk = t (т.е. не зависит от к-пост.)
xk+1 = xk - tÑf(xk)
Видно, что останавливаемся в любой точке, где Ñf(xk)=0.
Пример:
f(x) = ax2, a>0, x-скаляр
xk+1=xk - 2taxk = (1- 2at)xk
Отсюда
ç1-2atç<1Þ at<1- необходимое и достаточное условие существования предела
Если 0<tk<1/a - сходится,
tk>1/a - расходится,
tk=1/a - зацикливается.( tk=1/aÞ x1=x0-2x0= -x0 x2=x1-2x1= -x1=x0 и т.д.)
Выбор постоянного шага приводит к осложнениям. Оценим сходимость этого метода в общем случае.
Теорема (о сходимости метода градиентов)
Пусть f(x)- дифференцируема на Rn, Ñf(x) удовлетворяет условию Лифшица:
|| Ñf(x)-Ñf(y) ||£ L ||x-y || (*)
(||x2|| = Sxi2 ), f(x)- ограничена снизу
f(x)³ f* >-¥ (**)и 0< t< 2/L(***), L -const.
Тогда в методе xk+1= xk-Ñtf(xk), градиент стремится к нулю,
т.е. limÑf(xk) =0, при k®¥, а функция f(x) монотонно убывает f(xk+1)£f(xk). Точнее f(xk+1) £ f(xk)-t(1-tL/2)||Ñf(xk) ||2(градиент характеризует скорость убывания и множитель)
Известно из мат.анализа:
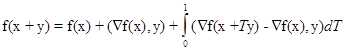(1)
Пусть x=xk, y= -tÑf(xk) (2)
Подставим (2) в(1):
f(xk+1)=f(xk)-t||Ñf(xk) ||2-t
-Ñf(xk),Ñf(xk))dT £
£ f(xk)-t+Lt2||Ñf(xk) ||2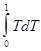 
=f(xk)-t(1-Lt/2) ||Ñf(xk) ||2
Обозначим a = t(1-Lt/2); a>0, так как (***)
Отсюда f(xk+1)£ f(xk)-a||Ñf(xk) ||2
Выразим f(xk+1) через f(x0)
Пусть k=0: f(x1)£ f(x0)- a||Ñf(x0) ||2
k=1: f(x2)£ f(x1)- a||Ñf(x1) ||2£ f(x0)- a||Ñf(x0) ||2 - a||Ñf(x1) ||2.........
f(xk+1)£ f(x0)- a
2
так как a>0, то 2£ a-1(f(x0)-f(xs+1))£ a-1(f(x0)-f*), для любого S
то есть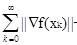 
<¥ ( сумма ограничена)Þ ||Ñf(xk) ||®0, то есть теорема доказана.
Замечание:
Сходимость градиента к нулю не гарантирует сходимости к минимуму.
Пример:
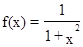, градиент сходится к нулю, но функция не имеет минимума.
Равенство градиента нулю- необходимое условие минимума, достаточное условие- положительность второй производной.
Таким образом доказана принципиальная сходимость метод при определенных условиях. Оценить скорость сходимости в общем случае можно для более узкого класса функции.