Вычисление площадей плоских фигур.

План

Приложения определенного интеграла

Лекция 10

1. Вычисление площадей плоских фигур
2. Вычисление длин дуг кривых
3. Вычисление объемов тел вращения
4. Вычисление площадей поверхностей тел вращения

Определенный интеграл от неотрицательной непрерывной функции равен площади соответствующей криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла, на этом основано его применение к вычислению площадей плоских фигур.

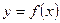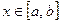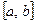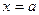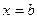
Площадь криволинейной трапеции, т. е. фигуры, ограниченной графиком неотрицательной непрерывной функции , , отрезком оси абсцисс и отрезками прямых , ,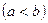вычисляется по формуле

. (10.1)

Если функция 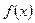конечное раз меняет знак на отрезке 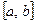, то интеграл по всему отрезку 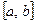на сумму интегралов по частичным отрезкам. Интеграл будет положителен на тех отрезках, где 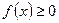, и отрицателен там, где 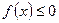. Интеграл по всему отрезку 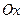даст разность площадей, лежащих выше и ниже оси. Для того, чтобы получить сумму площадей, необходимо найти сумму абсолютных величин интегралов по указанным выше отрезкам или вычислить интеграл:

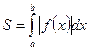(10.2)

Пример 10.1.

Вычислить площадь фигуры, ограниченной косинусоидой 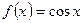, осью 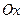и прямыми .