Комплексные числа

В арифметике и алгебре рассматривают различные действия над числами: арифметические (сложение, вычитание, умножение, деление), возведение в степень, извлечение корня и т.д. Только два действия – сложение и умножение – безусловно выполнимы в области натуральных чисел: сумма и произведение натуральных чисел также натуральные числа. Однако в области арифметики натуральных чисел уже вычитание не всегда выполнимо – для возможности образования разности двух натуральных чисел множество нужно дополнить до множества целых чисел , введя в него ноль и целые отрицательные числа. Такие операции как деление и извлечение корня становятся выполнимыми только после расширения рассматриваемой числовой области: множество целых чисел должно быть, соответственно, дополнено вначале до множества за счет введения рациональных чисел, а потом и до множества действительных чисел за счет введения иррациональных чисел.

Этот процесс можно схематически изобразить цепочкой , где , , , обозначают соответственно множества натуральных, целых, рациональных и действительных чисел. Причем каждая последующая числовая система сохраняет все основные свойства предыдущей и обладает рядом новых полезных свойств. Так, в можно только складывать и умножать, в можно уже вычитать, в ‑ делить. В множестве действительных чисел можно извлекать корни любой степени из положительных чисел, хотя в даже число не имеет смысла. Но и в множестве действительных чисел такое простое уравнение не имеет решений. Так как многие задачи практики приводят к алгебраическим уравнениям, требуется построить новое множество, содержащее множество действительных чисел и решение любого алгебраического уравнения. Символом , который называется мнимой единицей, обозначим корень уравнения , или . Множество , которое представляет собой множество всех двучленов вида , называется множеством комплексных чисел. Действительное число 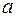называется действительной частью комплексного числа , ‑ мнимой частью или коэффициентом при мнимой единице. Два комплексных числа и будут равны тогда и только тогда, когда . При этом действительные числа рассматриваются как частный случай комплексных чисел, мнимая часть которых равна нулю (). Комплексное число равно нулю тогда и только тогда, когда равны нулю его действительная и мнимая части.

Операции сложения, вычитания и умножения над числами вида производятся по обычным правилам алгебры с единственным дополнительным условием: