Дивергенция поля в декартовой системе координат.

Замечание

-напряженность в данной точке пространства и плотность в этой же точке пространства.

-напряженность в одном месте, а заряд в другом месте.

Надо различать поле от внешних источников и поле, создаваемое зарядом, попавшим внутрь поверхности!

Нам теперь нужно записать оператор div в более явной форме, чтобы он мог служить инструментом для вычисления дивергенции произвольного поля 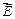. Перейдем к декартовой системе координат. Рассмотрим в декартовой системе координат произвольную точку и окружим ее элементарным прямоугольным параллелепипедом, который будет нам служить гауссовой поверхностью. Посчитаем поток вектора 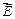через поверхность нашего параллелепипеда. Т.к. параллелепипед очень маленький, поле, пронизывающее отдельную его грань, можно считать однородным.

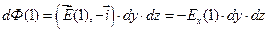
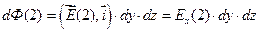
Приращение 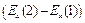может быть представлено в виде 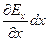, т.к. наш параллелепипед – очень маленький ,то есть грани близко к друг другу, поэтому конечное приращение можно задать через скорость изменения поля вдоль направления 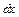(как быстро изменяется 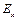при движении по )

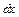Аналогично можно получить соотношения для других пар потоков:

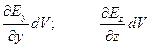
Тогда мы приходим к следующему результату: элементарный поток через всю замкнутую поверхность может быть записан в виде:

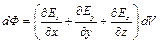
Ранее нами был введен оператор 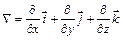- «набла» или оператор Гамильтона .

Используя его, можно записать: 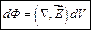, где

Учитывая полученную ранее формулу , где , можно записать:

- теорема Гаусса в дифференциальной форме.

3.5. ПРИМЕРЫ (задача на применение теоремы Гаусса).

Пример.1 Найдем поле 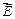однородно заряженного по объему с плотностью бесконечно длинного прямого цилиндра круглого сечения.

1) Рассмотрим напряженность поля в точках и попытаемся его найти с использованием теоремы Гаусса. Используем интегральную форму теоремы Гаусса. Выберем гауссову поверхность, которая должная удовлетворять следующим требованиям:

· поверхность должна содержать в себе рассматриваемую точку

· поверхность не должна быть заряжена (т.к. у нас конечная плотность распределения заряда, проведем гауссову поверхность между частицами, содержащими заряд)

· поверхность нужно выбирать так, чтобы легко было найти поток через эту поверхность

Для того, чтобы выбрать удобную гауссову поверхность, нужно что-то знать про то поле, величину которого мы собираемся искать. Перед тем как записывать теорему Гаусса, попытаемся определить ориентацию поля в рассматриваемой точке. Пусть вектор поля в этой точке ориентирован совершенно произвольно, тогда разложим его на 3 составляющие ,и так, как это показано на рисунке.

Пусть . Т.к. точка выбрана произвольно, т.е. на любой высоте (стержень бесконечно длинный) на расстоянии r от оси симметрии поле должно быть одинаково из соображений переносной симметрии. Пусть в нашей точке существует поле , а в точке на некоторой высоте над ней поле не такое же. Тогда возьмем и сместим наш цилиндр в вертикальном направлении. Тогда в выбранной точке поле должно бы измениться, но т.к. цилиндр бесконечно длинный, ничего в конфигурации нашей картинки не изменилось и поле меняться не должно. Получили противоречие. Тогда поток через нижнее основание выбранной нами гауссовой поверхности (маленького цилиндра, расположенного внутри нашего, поле которого мы и ищем) будет отрицательным, через верхнее – точно такой же по величине, но положительный, т.е. в сумме эти два слагаемых дадут ноль. А через боковую поверхность поток поля также равен нулю, потому что силовые линии перпендикулярны вектору нормали к поверхности. Т.е. суммарный поток через замкнутую поверхность =0, что противоречит теореме Гаусса (заряд внутри поверхности есть, а его потока через поверхность нет). Значит

Пусть , тогда оно направлено так, как показано на рисунке (это вид сверху на цилиндр) во всех точках цилиндра на расстоянии r от оси симметрии цилиндра. Тогда мы берем теорему о циркуляции электрического поля и считаем линейный интеграл от скалярного произведения , и ясно видим, что этот интеграл нулю не равен, потому что на каждом маленьком перемещении это скалярное произведение будет давать ненулевой вклад одного и того же знака, т.е. электрическое поле совершает работу по переносу заряда. А т.к. мы рассматриваем покоящиеся заряды, то

циркуляция должна быть равна нулю. Пришли к противоречию. существовать не может.

Значит поле создается только составляющей .

Теперь выберем подходящую гауссову поверхность (см. рисунок выше). Теперь мы можем посчитать нужный нам интеграл:

Два нулевых слагаемых после первого знака равенства – потоки через верхнюю и нижнюю крышки нашего цилиндра, т.к. вектор поля перпендикулярен векторам нормали к этим поверхностям.

, или в векторном виде:

2) Рассмотрим напряженность поля в точках .

Делаем все точно также: берем произвольную точку в пространстве, пытаемся понять, как направлено поле, которое мы ищем, основываемся на рассуждениях от противного, а также на теореме о циркуляции электрического вектора и теореме о потоке. В качестве гауссовой поверхности выберем цилиндр большего радиуса чем тот, поле которого мы ищем.

Проделав все вышесказанное, получим: