Модель 1.2. Электрическое поле точечных зарядов

Вопрос из ОРОКСА

Две линии напряженности электрического поля не могут пересекаться в одной точке. Можно ли утверждать, что две эквипотенциальные поверхности также не могут пересекаться в одной точке?

Ответ: Две эквипотенциальные поверхности могут пересекаться в одной точке при условии, что напряженность поля в этой точке равна нулю. В самом деле, вектор напряженности определяет направление нормали к каждой эквипотенциальной поверхности. Так как поверхности пересекаются, в точке пересечения их нормали не совпадают, а значит, электрическое поле не может иметь определенного направления. Это возможно только при нулевом значении величины поля.

Компьютерная модель демонстрирует картину силовых линий и эквипотенциальных поверхностей точечного заряда и системы из двух точечных зарядов. Можно изменять величины зарядов и их знаки, а также расстояние между зарядами. При установке курсора в любой точке и нажатии левой клавиши мыши компьютер высвечивает на дисплее значения модуля вектора напряженности электрического поля 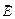и потенциала φ в данной точке. Следует обратить внимание, что в электрическом поле двух точечных зарядов возможны сферические эквипотенциальные поверхности.

2.7. Примеры вычисления потенциала

Рассмотрим вычисление потенциала поля, созданного некоторыми заряженными телами.

Рис.3. Расположение точки наблюдения А по отношению к точечному источнику поля q

1.Пример Точечный заряд. Используя соотношения (1) и (4) и совмещая точку 1 с точкой наблюдения А (рис.3), а точку 2 удаляя на бесконечность, получим

(7)

Замечание. До сих пор использовалось понятие векторного поля - поля векторов 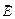(каждой точке пространства ставится в соответствие вектор 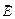). Представление о потенциале как функции точки пространства позволяет ввести понятие скалярного поля - поля чисел (каждой точке пространства ставится в соответствие, с точностью до произвольной аддитивной постоянной, число ). Поэтому в дальнейшем кроме понятий электростатическое поле и поле 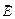, будем использовать понятие поля.

2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.

Наша задача найти как функцию .

Как уже было показано для бесконечно длинной нити:.

Выберем где-нибудь точку из которой мы стартуем, к примеру в точке , то

.

Договоримся, что в точке старта потенциал равен нулю: , тогда

.

 

Это при такой нормировке. Если в такой задаче нормировать , то получим ,то есть все потенциалы во всех точках бесконечно большие. Кому нужна такая нормировка? Если Вас интересует какой-то конкретный пространственный диапазон, то нормировать надо где-то вблизи этой области, тогда все потенциалами будут конечными приятными числами. От бесконечной нити нельзя уйти на бесконечность, по этой же причине не следует ожидать хорошего результата от как суммы потенциалов точечных фрагментов нити, каждый из которых нормирован условием.

 

3.Пример. Потенциал поля точечного диполя (первый способ).

Итак, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.

Давайте искать потенциал этой точки наблюдения.

Во первых, принцип суперпозиции.

Во-вторых, как известно

.

Учтя, что есть проекция вектора на и то, что расстояние до диполя очень велико, то

Потенциал поля точечного диполя (второй способ).

Используем готовую формулу для напряженности поля:

. Вот такое выражение мы с вами в свое время вывели. Обопремся на него.

Давайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор показаны на рисунке. С учетом некоторых соотношений (5) примет вид:

 

Определение вектора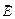точечного диполя из в полярной системе координат.

Оператор запишется в полярной системе координат так:

Орты координатных осей декартовой и полярной систем координат (см.рис.)

4.Пример

См. Иродов задача 3.38. (часть2)

Показать, что потенциал диполя с электрическим моментом может быть представлен как, где –радиус вектор. Найти с помощью этого выражения модуль напряженности электрического поля диполя как функцию и .

 

- это уже показали выше, отсюда, раскрывая скалярное произведение и продифференцировав формулу для потенциала, мы получим 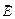.