Геометрическая интерпретация производной.
Пусть на плоскости xOy задана кривая, описываемая уравнением 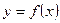 . Проведём касательную к кривой в точке
. Проведём касательную к кривой в точке 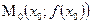 . Возьмём на кривой точку M1 и проведём секущую M0M1 (рис. 15.1). При изменении точки M1 положение секущей будет меняться.
. Возьмём на кривой точку M1 и проведём секущую M0M1 (рис. 15.1). При изменении точки M1 положение секущей будет меняться.
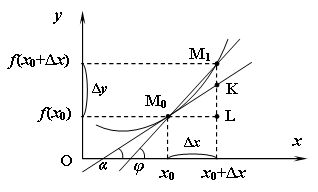
| Рис. 15.1. |
Определение 15.2. Если при стремлении точки  к фиксированной точке
к фиксированной точке 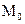 секущая
секущая 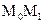 не зависимо от способа стремления точки
не зависимо от способа стремления точки  к точке
к точке 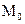 стремится к одному и тому же предельному положению, то прямая, являющаяся этим предельным положением, называется касательной к кривой в точке
стремится к одному и тому же предельному положению, то прямая, являющаяся этим предельным положением, называется касательной к кривой в точке 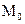 .
.
Получим уравнение этой касательной. Обозначим координаты точки M1 через 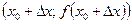 и пусть
и пусть 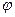 – угол наклона секущей к оси Ox. Тогда (см. рис. 15.1) угловой коэффициент секущей M0M1 равен
– угол наклона секущей к оси Ox. Тогда (см. рис. 15.1) угловой коэффициент секущей M0M1 равен
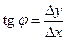 . (15.3)
. (15.3)
Если же устремить точку M1 к точке M0, то есть устремить 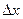 к нулю, то в случае существования производной
к нулю, то в случае существования производной 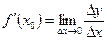 угол
угол 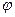 будет стремиться к некоторому пределу
будет стремиться к некоторому пределу 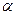 , где
, где  . Следовательно, прямая, составляющая с положительным направлением оси Ox угол
. Следовательно, прямая, составляющая с положительным направлением оси Ox угол 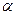 и проходящая через точку M0 и будет касательной. Её угловой коэффициент
и проходящая через точку M0 и будет касательной. Её угловой коэффициент 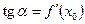 .
.
Запишем уравнение касательной к графику 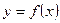 в точке
в точке 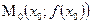 :
:
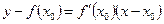 . (15.4)
. (15.4)
Определение 15.3. Прямая называется перпендикулярной к кривой в точке 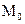 , если она перпендикулярна касательной к кривой в точке
, если она перпендикулярна касательной к кривой в точке 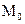 . Эта прямая называется также нормалью к этой кривой.
. Эта прямая называется также нормалью к этой кривой.
Угловой коэффициент нормали к кривой в точке M0 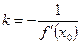 при
при 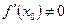 , и уравнение нормали к графику функции, проходящему через точку
, и уравнение нормали к графику функции, проходящему через точку 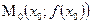 запишется в следующем виде:
запишется в следующем виде:
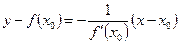 . (15.5)
. (15.5)
Если 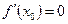 , то уравнение нормали
, то уравнение нормали 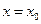 .
.
☼ Замечание 15.1. Если в точке 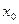
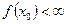 и
и 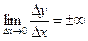 , то касательная к кривой
, то касательная к кривой 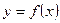 в точке
в точке 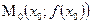 существует, она вертикальна и её уравнение
существует, она вертикальна и её уравнение 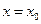 . Уравнение соответствующей нормали
. Уравнение соответствующей нормали  .☼
.☼