Понятие состояния
В процессе общей характеристики физики как основной отрасли естествознания часто употреблялся термин “состояние физической системы”. Рассмотрим его более подробно.
Категория состояния сложилась в античной философии. В науке она впервые нашла широкое применение в ньютоновской механике. Здесь состояние рассматривалось как количественная характеристика механического движения. Значение механики Ньютона для физики далеко не в последнюю очередь определяется именно тем, что Ньютон первым понял: состояние систем материальных точек в любой заданный момент времениt полностью определяется значением их координат и импульсов (а не ускорениями, взаимодействиями и т.д.). Зная эти величины в момент t, можно определить эволюцию системы под влиянием известных сил во все последующие моменты времени, решив систему уравнений Ньютона:

Состояние физической системы — это конкретная определенность системы, однозначно детерминирующая ее эволюцию во времени. Для задания состояния системы необходимо: 1) определить совокупность физических величин, описывающих данное явление и характеризующих состояние системы, — параметры состояния системы; 2) выделить начальные условия рассматриваемой системы (зафиксировать значения параметров состояния в начальный момент времени); 3) применить законы движения, описывающие эволюцию системы.
Параметрами, характеризующими состояния механистической системы, являются совокупность всех координат и импульсов материальных точек, составляющих эту систему. Задать состояние механической системы, значит, указать все координаты r1(х1, у1, z1) и импульсы Р1 всех материальных точек. Основная задача динамики состоит в том, чтобы, зная начальное состояние системы и законы движения (законы Ньютона), однозначно определить состояние системы во все последующие моменты времени, то есть однозначно определить траектории движения частиц. Траектории движения получаются путем интегрирования дифференциальных уравнений движения. Траектории движения дают полное описание поведения частиц в прошлом, настоящем и будущем, то есть характеризуются свойствами детерминированности и обратимости. Здесь полностью исключается элемент случайности, все заранее жестко причинно-следственно обусловлено. Считается, что задать начальные условия можно абсолютно точно. Точное знание начального состояния системы и законов движения ее предопределяет попадание системы в заранее выбранное, «нужное» состояние.
Представим себе тело, которое с точки зрения физики можно назвать макроскопическим. Это может быть газ в сосуде, песчинка, кусочек железа и т.д. Другими словами - это любое тело, состоящее из очень большого числа частиц.
На протяжении более 200 лет считалось, что механика Ньютона описывает перемещение тел любых размеров, т.е. любых размеров масс друг относительно друга. Но с этими телами происходят и другие изменения, не связанные с их макроскопическими перемещениями. В первую очередь, это тепловые процессы. Тела могут нагреваться и остывать. При этом их температура меняется.
Температура - очень важная характеристика состояния тел. Ее изменения могут вызывать изменения тел гораздо более существенные, чем простые перемещения из одной области пространства в другую. Так, газ может превратиться в жидкость, жидкость - в твердое тело (или наоборот), и т.д.
Подобного рода процессы описываются термодинамикой.
Термодинамика. В термодинамике тепловые процессы рассматриваются без учета молекулярного строения тел. Поэтому состояние термодинамической системы описывается совсем иначе, чем в механике. В простейшем случае газа основными величинами, задающими состояние системы, являются давление, объем и температура. Эти величины называются термодинамическими параметрами. Между ними существует связь, даваемая уравнением состояния. Состояние системы полностью характеризуется значениями независимых параметров. Число таких параметров называют числом степеней свободы термодинамической системы.
Первое и второе начала термодинамики вводят две однозначные функции состояния: внутреннюю энергию и энтропию. В классической термодинамике рассматриваются лишь состояния равновесия и равновесные обратимые (бесконечно медленные) процессы. Эволюция реальных систем во времени фактически не рассматривается. С помощью термодинамики можно лишь установить однозначные связи между термодинамическими параметрами различных равновесных состояний.
Неравновесные процессы изучаются в термодинамике необратимых процессов. В этой теории состояние системы характеризуется локальными термодинамическими функциями координат и времени. К их числу относятся: плотность массы, плотность импульса, температура, давление, плотность внутренней энергии или энтропии. Для локальных термодинамических функций записываются уравнения переноса, выражающие сохранение массы, импульса и энергии в движущейся среде. Эти уравнения совместно с уравнением состояния и калорическим уравнением, дающим зависимость энергии от давления и температуры, позволяют по начальным значениям локальных термодинамических функций проследить их эволюцию во времени.
Электродинамика. В электродинамике Максвелла объектом исследования является электромагнитное поле. Состояние электромагнитного поля характеризуется на-пряженностями электрического поля E(r, t) и магнитного поля Н(r, t). По известным электрическим и магнитным свойствам вещества, задаваемым диэлектрической проницаемостью e и магнитной проницаемостью m определяются две другие характеристики поля: электрическая индукция D(r, t) и магнитная индукция B(r, t).
Уравнения Максвелла для этих четырех векторов позволяют по заданным начальным значениям полей E и H внутри некоторого объема и по граничным условиям
для тангенциальной составляющей либо E, либо Н однозначно определить величину электромагнитного поля в любой последующий момент времени.
Аналогично характеризуется состояние электромагнитного поля в теории Лоренца, описывающей микроскопические электромагнитные процессы. Основные уравнения этой теории - уравнения Максвелла - Лоренца, связывающие движение отдельных заряженных частиц с созданным ими электромагнитным полем, подобны уравнениям Максвелла
Итак, классическая физика считала, что состояние физической системы всегда задается физическими параметрами. Это, например, координата, импульс, температура, вектор намагничивания и т.д. Состояние системы - это значение таких параметров системы в определенный момент времени, которые позволяют решать определенные классы задач по отношению к данной системе. Бессмысленно задавать состояние физической системы безотносительно к классу поставленных по отношению к системе задач. Какие именно параметры характеризуют конкретное состояние системы определяется законами, на основании которых и решаются поставленные задачи.
Любая система может быть описана лишь с какой-то степенью приближения. Это касается и набора параметров, задающих состояние системы, и значения параметров, которые всегда, конечно, приближенны. Другими словами, всегда существует разница между истинным состоянием системы и описанием этого состояния.
Всевозможные состояния, в которых может находиться то или иное вещество, прежде всего, разбиваются на так называемые агрегатные состояния: твердое, жидкое и газообразное. Эти состояния выделяются по основным физическим свойствам вещества.
Следует учесть, что у некоторых веществ нет резкой границы между различными агрегатными состояниями. Например, при нагревании стекла происходит постепенное его размягчение, и невозможно установить, когда оно переходит из твердого состояния в жидкое. При очень большом внешнем давления твердые металлы начинают “течь”, т.е. подобно жидкости, принимают форму сосуда, в котором они находятся.
Различные состояния одного и того же вещества можно отличать друг от друга также и по значениям физических величин, которые характеризуют эти состояния, например, по значениям объема, температуры и давления. Поэтому каждому агрегатному состоянию вещества соответствует бесконечное множество различных состояний, которые отличаются друг от друга различными значениями объема, давления, температуры и других физических величин. При изменении этих величин вещество переходит из одного состояния в другое, оставаясь твердым, жидким или газообразным.
Физические величины, характеризующие то или иное состояние вещества, иногда называют параметрами состояния. Основные параметры: объем V, внешнее давление Р и температура Т. Если между параметрами состояния существует какое-нибудь определенное однозначное соотношение, которое сохраняется при переходе из одного состояния в другое, то это соотношение называется уравнением состояния. Например, для разряженных газов соблюдается уравнение:
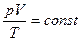
Это соотношение связывает между собой значения объема, давления и температуры для множества отличающихся друг от друга состояний данной массы газообразного вещества. Для других агрегатных состояний - твердого и жидкого - такие простые соотношения между параметрами не найдены.
Важным свойством термодинамических систем является существование у них равновесных состояний, в которых они могут пребывать сколь угодно долго. Для газа, заключенного в некотором сосуде, равновесным является состояние, в котором температура, давление и плотность (или число молекул в единице объема) в пределах объема газа одинаковы. Если в каком-нибудь месте этого объема вызвать местное нагревание или сжатие, то в системе начнется процесс выравнивания температуры и давления. Этот процесс будет происходить в течение того времени, пока имеется внешнее воздействие. Однако только после прекращения этого воздействия процесс выравнивания приведет систему к новому равновесному состоянию.
Состояния изолированных термодинамических систем, в которых они, несмотря на отсутствие внешних воздействий, не могут пребывать в течение конечных промежутков времени, называются неравновесными. Система, первоначально находящаяся в неравновесном состоянии, с течением времени переходит в равновесное состояние. Время перехода из неравновесного состояния в равновесное называется временем релаксации.
В физике широко используется понятие стационарного состояния. Состояние физической системы, при котором некоторые существенные для характеристики системы величины не меняются со временем называется стационарным. Например, состояние потока жидкости стационарно, если скорость движения (и другие характеристики) остаются в каждой точке пространства неизменными.
В квантовой механике стационарным состоянием называется состояние, в котором энергия имеет определенное значение. Стационарное состояние может быть равновесным и неравновесным.
Стационарным состоянием открытой системы является подвижное равновесие, при котором все макроскопические величины остаются неизменными, но непрерывно продолжаются макроскопические процессы ввода и вывода вещества.
Состояния микрообъектов методами классической физики описать нельзя. Это очевидно хотя бы из соотношения неопределенностей. Принцип неопределенности, установленный В. Гейзенбергом в 1927 г., записывается так:

где 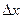 выступает как неточность (неопределенность) значения координаты х частицы;
выступает как неточность (неопределенность) значения координаты х частицы;
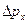 – как неопределенность компоненты Px ее импульса
– как неопределенность компоненты Px ее импульса 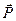 .
.
Принцип неопределенностей подчеркивает различие в описании состояния систем в классической и в квантовой теории. Мы уже неоднократно подчеркивали, что состояние классической материальной точки описывается с помощью координат и импульса. Квантовая же частица в состоянии с определенными координатами не обладает определенным импульсом. Иными словами, для квантовой частицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точное значение. Поэтому в квантовой теории состояние микрообъектов, как уже подчеркивалось, описывается принципиально по-новому – с помощью волновой функции.
Великий австрийский физик Эрвин Шрёдингер, проникшись идеей де Бройля о волнах материи, создал теорию, в которой дискретные стационарные состояния энергии уподоблялись стоячим волнам какой-либо системы. В аппарат квантовой теории прочно вошло в качестве ее основного уравнения – уравнение Шрёдингера относительно волновой функции Ψ. Сам Шрёдингер интерпретировал Ψ-функцию как реальный волновой процесс в пространстве и во времени, который, в конечном счете, должен приводить к отрицанию дискретных состояний и квантовых скачков. Однако дальнейшее развитие теории показало неадекватность подобных представлений, и волновая функция Ψ стала интерпретироваться как волна вероятности, а квадрат ее модуля — как мера вероятности обладания микрообъектом определенной координаты или в другой, дополнительной к первой, физической ситуации — определенного импульса. Итак, волновая функция получила статус волны вероятности, чем еще раз подчеркивается статистический, вероятностный характер поведения микрообъектов. Казалось бы, что о причинно-следственном описании движения объектов следует забыть. Однако это не так. Уравнение Шрёдингера описывает эволюции Ψ-функции с течением времени, является детерминированным и обратимым. Волновая функция представляет собой, полную характеристику состояния: зная волновую функцию Ψ, можно вычислить вероятность обнаружения определенного значения физической величины и средние значения физических величин.