Галилей
Классическая (ньютоновская) механика
Классическая (ньютоновская) механика изучает движение материальных объектов при скоростях, которые значительно меньше скорости света в вакууме.
Начало формирования классической механики связывают с именем итал. ученого Галилео Галилея (1564-1642). Он впервые перешел от натурфилософского рассмотрения природных явлений к научно-теоретическому.
Трудами Галилея, Кеплера, Декарта был заложен фундамент классической физики, а трудами Ньютона было построено здание этой науки.
1. установил основополагающий принцип классической механики – принцип инерции
Движение - собственное и основное, естественное состояние тел, тогда как трение и действие других внешних сил может изменить и даже прекратить движение тела.
2. сформулировал еще один основополагающий принцип классической механики – принцип относительности – Равноправие всех ИСО.
Согласно этому принципу внутри движущейся равномерно системы все механические процессы происходят так, как если бы система покоилась.
3. принцип относительности движения задает правила перехода от одной ИСО к другой.
Эти правила получили название галилеевых преобразований и состоят они в проецирование одной ИСО на другую.
Галилеевы преобразования предъявляют определенное требование к формулировке законов механического движения: эти законы должны быть сформулированы так, чтобы остались инвариантными в любой ИСО.
Пусть некоторое тело А отнесено к декартовой системе, координаты которой обозначены х,y,z , а нам нужно определить параметры тела в параллельной координатной системе со штрихами (xl,yl,zl). Для простоты будем определять параметры одной точки тела, и совместим координатную ось x1 с осью x. Примем также, что координатная система со штрихами покоится, а без штрихов – движется равномерно и прямолинейно. Тогда правила галилеевых преобразований имеют вид
x1= x-vt
y1=y
z1=z
t1=t
4. формулировка закона свободного падения (путь свободного падающего тела пропорционален ускорению, равному 9,81 м/с2.
Развивая и углубляя исследования Галилея, Ньютон сформулировал три закона механики.
1. Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения. Пока воздействие со стороны других тел не заставит его изменить это состояние.
Смысл первого закона состоит в том, что если на тело не действуют внешние силы, то существует система отсчета, в которой оно покоится. Но если в одной системе тело покоится, то существует множество других систем отсчета, в которых тело движется с постоянной скоростью. Эти системы называются инерциальными (ИСО).
Любая система отсчета, движущаяся равномерно и прямолинейно относительно ИСО также является ИСО.
2.Второй закон рассматривает результаты действия на тело других тел. Для этого вводится физическая величина, называемая силой.
Сила – это векторная количественная мера механического действия одного тела на другое.
Масса – мера инертности (инертность – способность тела оказывать сопротивление изменению его состояния).
Чем больше масса, тем меньше ускорение получит тело при прочих равных условиях.
ā= F/m.
Существует и более общая формулировка второго закона Ньютона для другой физической величины – импульса тела. Импульс – это произведение массы тела на его скорость:
P= mv
При отсутствии внешних сил импульс тела остается неизменным, иначе говоря, сохраняется. Такая ситуация достигается, если на тело не действуют другие тела, или их действие скомпенсировано.
3.Действия двух материальных тел друг на друга численно равны по величине силы и направлены в противоположные стороны.
F12= - F21
Действие сил осуществляется независимо. Сила, с которой несколько тел действуют на какое-либо другое тело, есть векторная сумма сил, с которыми они бы действовали отдельно.
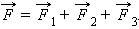
Это утверждение представляет собой принцип суперпозиции.
На законах Ньютона основана динамика материальных точек, в частности, закон сохранения импульса системы.
Сумма импульсов частиц, образующих механическую систему, называется импульсом системы. Внутренние силы, т.е. взаимодействия тел системы друг с другом на изменения полного импульса системы не влияют. Из этого вытекает закон сохранения импульса: при отсутствии внешних сил импульс системы материальных точек остается постоянным.
Другой сохраняющейся величиной является энергия – общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую.
Мерой изменения энергии является работа. В классической механике работа определяется как мера действия силы, которая зависит от величины и направления силы, а также от перемещения точки ее приложения.
Закон сохранения энергии: полная механическая энергия остается неизменной ( или сохраняется), если работа внешних сил в системе равна нулю.
В классической механике считается, что все механические процессы подчиняются принципу строгого детерминизма (детерминизм - это учение о всеобщей причинной обусловленности и закономерности явлений) который состоит в признании возможности точного определения будущего состояния механической системы ее предыдущим состоянием.
Ньютон ввел два абстрактных понятия – «абсолютное пространство» и «абсолютное время».
По Ньютону, пространство – это абсолютное неподвижное однородное изотропное бесконечное вместилище всех тел (то есть пустота). А время- это чистая однородная равномерная и прерывная длительность процессов.
В классической физике считалось, что мир можно разложить на множество независимых элементов экспериментальными методами. Этот метод в принципе неограничен, так как весь мир - это совокупность огромного числа неделимых частиц. Основа мира - атомы, т.е. мельчайшие, неделимые, бесструктурные частицы. Атомы перемещаются в абсолютном пространстве и времени. Время рассматривается как самостоятельная субстанция, свойства которой определяются ею самой. Пространство – это тоже самостоятельная субстанция.
Напомним, что субстанция - это сущность, нечто, лежащее в основе. В истории философии субстанция интерпретировалась по-разному: как субстрат, т.е. основа чего–то; что-то, что способно к самостоятельному существованию; как основание и центр изменения предмета; как логический субъект. Когда говорят, что время - субстанция, то имеют в виду, что оно способно самостоятельно существовать.
Пространство в классической физике абсолютно, что означает, что оно не зависит от материи и времени. Можно убрать из пространства все материальные объекты, а абсолютное пространство остается. Пространство однородно, т.е. все его точки эквивалентны. Пространство - изотропно, т.е. эквивалентны все его направления. Время тоже однородно, т.е. эквивалентны все его моменты.
Пространство описывается геометрией Евклида, согласно которой кратчайшим расстоянием между двумя точками является прямая.
Пространство и время бесконечны. Понимание их бесконечности было позаимствовано из математического анализа.
Бесконечность пространства означает, что какую бы большую систему мы не взяли, всегда можно указать на такую, которая еще больше. Бесконечность времени означает, что как бы долго ни длился данный процесс, всегда в мире можно указать на такой, который будет длиться дольше.
Из разрозненности и абсолютности пространства и времени вытекают правила галилеевых преобразований.
Из оторванности движущихся тел от пространства и времени вытекает правило сложения скоростей в классической механике: оно состоит в простом сложении или вычитании скоростей двух тел, движущихся относительно друг друга.
ux = u'x + υ, uy = u'y, uz = u'z.
Законы классической механики позволили сформулировать первую научную картину мира – механистическую.
Прежде всего, классическая механика выработала научное понятие движения материи. Теперь движение трактуется как вечное и естественное состояние тел, как основное их состояние, что прямо противоположно догалилеевой механике, в которой движение рассматривалось как привнесенное извне. Но вместе с тем в классической физике абсолютизируется механическое движение.
Деле классическая физика выработала своеобразное понимание материи, сведя ее к вещественной, или весовой, массе. При этом масса тел остается неизменной при любых условиях движения и при любых скоростях. Позже в механике утвердилось правило замещения тел идеализированным образом материальных точек.
Развитие механики привело к изменению представлений о физических свойствах объектов.
Классическая физика считала свойства, обнаруживаемые при измерении, присущими объекту и только ему (принцип абсолютности свойств). Напомним, что физические свойства объекта характеризуются качественно и количественно. Качественная характеристика свойства - это его сущность (например, скорость, масса, энергия и т.д.). Классическая физика исходила из того, что средства познания на изучаемые объекты не влияют. Для различных типов механических задач средством познания является система отсчета. Без ее введения нельзя корректно ни сформулировать, ни решить механическую задачу. Если свойства объекта ни по качественной, ни по количественной характеристике не зависят от системы отсчета, то они называются абсолютными. Так, какую бы систему отсчета для решения конкретной механической задачи мы не взяли, в каждой из них будут проявляться качественно и количественно масса объекта, сила, действующая на объект, ускорение, скорость.
Если же свойства объекта зависят от системы отсчета, то их принято считать относительными. Классическая физика знала лишь одну такую величину - скорость объекта по количественной характеристике. Это означало, что бессмысленно говорить, что объект движется с такой-то скоростью, не указывая систему отсчета: в разных системах отсчета количественное значение механической скорости объекта будет различно. Все же остальные свойства объекта были абсолютными и по качественной, и по количественной характеристикам.
Уже теория относительности вскрыла количественную относительность таких свойств, как длина, время жизни, масса. Количественная величина этих свойств зависит не только от самого объекта, но и от системы отсчета. Отсюда следовало, что количественная определенность свойств объекта должна быть отнесена не к самому объекту, а к системе: объект + система отсчета. Но носителем качественной определенности свойств по-прежнему оставался сам объект.