Выполнимость формулы алгебры логики
Все формулы алгебры логики делятся на три класс:
1. тождественно истинные или тавтологии:
2. тождественно ложные или противоречия;
3. выполнимые.
Формулу называют тождественно истинной (тавтологией), если она принимает значение истинно при любых значениях входящих в нее переменных.
Формула называется тождественно ложной (противоречие), если она принимает значение ложно при любых значениях переменных входящих в нее.
Формула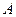 
называется выполнимой, если она принимает значение истинно хотя бы один раз на любом наборе значений входящих в нее переменных и не является тождественно истинной..
Тождественно истинная формула не имеет СКНФ, а ложная СДНФ.
ПРИМЕР
Формула 
является тождественно ложной:
| 
|
|
Формула 
является тождественно истинной:
|
|
|
|
Формула 
является выполнимой:
|
| 
|
|
Очевидно, что тождественно ложная формула не имеет СДНФ, а тождественно истинная – СКНФ. Выполнимая формула алгебры логики имеет СДНФ и СКНФ,