М.9. РАСЧЕТ ДЕФОРМАЦИЙ ОСНОВАНИЙ СООРУЖЕНИЙ

М.8.12. Каким образом распределяются напряжения s z под подошвой жесткого штампа? Чему равны реактивные напряжения под краем штампа? Чему равны реактивные напряжения под серединой ленточного и круглого жестких штампов?

В соответствии с решением задачи об абсолютно жестком штампе, плотно примыкающем к поверхности упругого полупространства и нагруженном симметричной нагрузкой, эпюра реактивных давлений имеет седлообразное очертание с минимальной ординатой в середине и наибольшими ординатами реактивных давлений, равными бесконечности, у краев. Эти бесконечно большие давления у краев штампа вызывают необходимый из постановки задачи "излом" поверхности в краевых точках. Если среднее давление под подошвой штампа равно p, то под серединой ленточного штампа ордината эпюры равна 0,637p (то есть 2p/p ), а под круглым штампом 0,5p (рис.М.8.12).

М.8.13*. Что следует сделать, чтобы проверить условие равновесия, пользуясь эпюрой реактивных напряжений под подошвой штампа?

Для этой цели следует найти объем эпюры реактивных давлений (для плоского штампа на единицу длины), и этот объем должен равняться суммарной внешней нагрузке, действующей на штамп, то есть сумма проекций на вертикальную ось действующих сил должна равняться нулю (условие равновесия).

 

М.9.1. Какой обычно практически считается эпюра приложения нагрузки на основание? Каким образом учитывается заглубление фундамента в основание?

Эпюра приложения нагрузки на основание считается обычно равномерной, если нагрузка симметричная, или трапецеидальной, если нагрузка приложена с эксцентриситетом.

Заглубление фундамента обычно учитывается в форме равномерной вертикально действующей пригрузки по краям фундамента.

М.9.2*. Какой вид имеет эпюра реактивных напряжений под жестким штампом? Каким образом на нее влияют области пластической деформации?

Эпюра реактивных напряжений (давлений) под жестким штампом, полученная из решения теории упругости, имеет форму "седла" с максимумом под краями (ординаты равны бесконечности) и минимумом в середине (менее средней величины давления). Поскольку грунт (да и любой материал) не может воспринимать бесконечно больших давлений, то под краями начинают развиваться области пластической деформации, а ординаты эпюры реактивных давлений превышать предельные значения не могут. Но чтобы выполнить условие равновесия, то есть чтобы не нарушался объем (площадь) эпюры, повышаются ординаты эпюры во внутренней ее части (рис.М.9.2,а).

В случае эксцентричного приложения внешней нагрузки вместо прямоугольной эпюры мы имеем трапецеидальную (рис.М.9.2,б) и применительно к ней делаются те же построения, какие показаны на рис.М.9.2,а.

Рис.М.9.2. Эпюры реактивных давлений: а - случай центральной нагрузки; б - случай внецентренного нагружения: 1 - эпюра по решению теории упругости; 2,3 - трансформация эпюры с ростом пластических деформаций; 4 - вид эпюры, принимаемый в практических расчетах; 5 - осадка поверхности основания; 6, 7 - максимальные и минимальные краевые давления; 8 - центр эпюры реактивных давлений

М.9.3. Какой вид имеет кривая зависимости "осадка-нагрузка" для штампа и какой вид ей придают при расчете осадки?

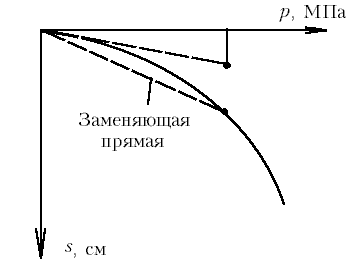
Кривая зависимости "осадка-нагрузка" для штампа имеет вид, представленный на графике. При расчете осадки эту кривую на интересующем нас участке заменяют прямой (рис.М.9.3).

Рис.М.9.3. Зависмость осадки штампа от нагрузки

М.9.4. Что называется "осадочным" давлением и какое обоснование дается тому, что осадка рассчитывается не на полную величину давления?

Осадочным давлением p_o именуется разность давлений полного передаваемого основанию через подошву фундамента и "бытового" - природного давления, которое испытывает грунт на отметке заложения подошвы фундамента. Таким образом, осадка рассчитывается не на полную величину прикладываемого давления, а на уменьшенную. Обоснованием для этого служит то, что осадки в грунтовом массиве от веса вышележащей толщи уже завершились, а упругие деформации подъема незначительны, также как и повторные осадки (упругие и остаточные) при нагрузке в пределах давления от вышележащей толщи грунта. Поэтому кривая "осадки-нагрузки" будет иметь вид, показанный на рис.М.9.4.