СУ заданным углом курса (управление разворотом через крен)
СУ заданным углом курса (плоский разворот самолета)
СУ заданным углом курса
Автоматическое управление курсовым движением С-та может быть реализовано одним из следующих способов:
- плоский разворот без крена с помощью dН;
- разворот с креном с помощью dЭ и dН , в том числе координи-рованный разворот с углом скольжения равным нулю.
Плоский разворот - управление курсом, воздействием на руль направления. При таком способе руль направления создаёт скольжение, которое в свою очередь создаёт поперечную, искривляющую траекторию силу 
.
Для осуществления плоского разворота необходимо отклонять элероны для стабилизации угла крена (для ликвидации момента 
(см. первое уравнение в (3.20)).Т.е. в плоском развороте руль направления используется для создания скольжения, а элероны для ликвидации крена(см.Рис. ниже)
Плоский разворот используется для решения специальных задач, связанных с плоским движением С-та при “жесткой” стабилизации его по крену ( 
=0) например, при аэрофотосъемке или при небольших доворотах при посадке на ВПП. Для обеспечения “жесткой” стабилизации С-та по крену используется одна из схем рассмотренных выше систем стабилизации по углу крена. При этом движение С-та по рысканию описывается системой уравнений (3.19).
Закон управления идеального статического автомата курса имеет вид:
(3.21)
Для приближённого анализа движения рыскания и предварительного выбора передаточных чисел используют уравнения изолированного движения рыскания (3.19). Добавив к уравнениям (3.19) закон управления (3.21), получают систему уравнений замкнутого контура «самолёт-автомат курса». Структурная схема контура показана на Рис.
Передаточная функция самолёта по углу рыскания, полученная из уравнений (3.19), имеет вид:
Выбор передаточных чисел 
и 
. Сначала выбирается передаточное число методом стандартных коэффициентов. Для этого рассматривается внутренний контур, обведённый на Рис. выше пунктиром. Он представляет собой контур демпфирования рыскания с ПФ:
(3.23)
Передаточная функция (3.23) соответствует передаточной функции колебательного звена, соединённого последовательно с форсирующим звеном. Если задаться оптимальным демпфированием колебательного звена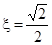
,то передаточное число определится по формуле:
Выбрав , можно для выбора передаточного числа воспользоваться методом ЛАЧХ. Структурную схему Рис. выше можно преобразовать в одноконтурную
 | |||||||||
 | |||||||||
 | |||||||||
| |||||||||
 | |||||||||
 | |||||
| |||||
 | |||||
Для получения оптимального переходного процесса частота среза должна выбираться в пределах ωc=-(0.9—0.95)Zβ. При этом частота среза лежит на участке с наклоном –20 [дб/дек] и будет равной:
(3.25)
Из выражения (3.25) находят:
(3.26)
Время переходного процесса при таком передаточном числе можно оценить по формуле:
.
ПФ замкнутой системы определяется выражением (3.27)
Типичный переходный процесс системы имеет вид
| |||
 | |||
Всплеск в начале процесса тем меньше выражен, чем больше собственная частота 
внутреннего контура по сравнению с частотой w = Кy.
Управление курсом воздействием на элероны называется разворотом с креном. При таком способе разворота в качестве силы, разворачивающей вектор скорости в горизонтальной плоскости, используется проекция подъёмной силы на эту плоскость.
Этот способ управления широко распространен по двум причинам:
- более высокая эффективность, вызванная значительно большей по величине разворачивающей вектор скорости проекции подъемной силы
 |
на горизонтальную плоскость в сравнении с боковой аэродинамической силой
при плоском развороте (несущая площадь горизонтального оперения значительно больше вертикального);
- отсутствуют боковые силы, действующие на летчика и пассажиров, при управлении без скольжения.
Разворот с креном без скольжения называется координированным. Для ликвидации (или уменьшения) скольжения, а также демпфирования колебаний по рысканию используется руль направления.
При этом движение С-та вблизи горизонтальной плоскости может быть описано следующей системой линеаризованных уравнений бокового движения в предположении отсутствия углов атаки и тангажа, малости спиральных моментов)
(3.28)
При развороте с креном сигнал отклонения от заданного курса подается на элероны. Законы управления каналов элеронов и руля направления статической системы стабилизации принимают вид:
(3.29)
При координированном развороте в канал руля направления подаётся сигнал перекрёстной связи по крену. Закон управления (3.29) принимает вид:
|
|
выбирают из условия 
на всех этапах разворота. Для его выбора используется система уравнений (3.28), дополненная законами управления (3.30), (3.31). Полученную систему уравнений представляют в области изображения по Лапласу
или
, где А и В - матрицы коэффициентов:
|
|
 |  |
В результате получают
|
 |
Чтобы выполнялось условие
, коэффициенты В1, В2, В3 также должны быть равны нулю. Последнее реализовать технически трудно, поэтому на практике ограничиваются требованием отсутствия скольжения только в установившемся развороте, для чего достаточно лишь выполнение условия
В =0, что соответствует
(3.37)
Передаточное число определяют, исходя из требований к контуру демпфирования изолированного канала РН (см. п.3.3.1), по формуле (3.24):
При выборе передаточного числа 
используется упрощеная система уравнений самолёта в виде (3.7).
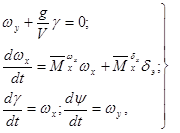
Так как переменная 
в этой системе не фигурирует, то для получения системы уравнений контура стабилизации угла рыскания достаточно к этой системе добавить закон управления
.
В итоге получим систему уравнений, описывающих динамику координированного разворота. Этой системе соответствует структурная схема, показанная на Рис.
Из этой схемы можно получить передаточную функцию замкнутой системы:
(3.39)
В ПФ (3.39) неизвестно только передаточное число (выбор передаточных чисел Kwx и Кg см. синтез системы стабилизации угла крена). Эта передаточная функция не имеет нулей, поэтому характер переходной функции полностью определяется распределением её полюсов, т.е. корней характеристического уравнения. Поэтому для предварительного выбора передаточного числа можно воспользоваться корневыми методами. В частности, можно использовать понятие степени устойчивости η - расстояние от мнимой оси до ближайшего корня или ближайшей пары корней. Если учесть, что при выборе передаточных чисел системы стабилизации крена было выбрано оптимальное демпфирование ξ=0.707, а переходный процесс по крену значительно короче, чем переходный процесс по курсу, можно считать, что в данном случае ближайший к мнимой оси корень – действительный. Известно, что для такого случая можно получить приближённую зависимость между временем переходного процесса tр и степенью устойчивости η:
Где m-половина ширины трубки, по которой оценивается длительность переходного процесса. Если m=0.05, то
 |
Задавшись временем tр, можно получить требуемое значение η по формуле:
Подставив S = -η в характеристическое уравнение 
и представим 
через (3,39), можно получить:
.