Маршруты, пути, цепи, циклы
Тема 4.2. Маршруты и деревья
Резюме по теме
Вопросы для повторения
1.Чему посвящен раздел дискретной математики, изучающий теорию графов?
2.В чем отличие ориентированного и неориентированного графов?
3.Дайте определение графа?
4.В чем заключается смысл отношения инцидентности?
5.Локальная степень вершины графа это?
6.В каком случае графы называются изоморфными?
7.Назовите способы задания графов?
8.Перечислите отличия матрицы инцидентности и матрицы смежности?
9.Когда граф называется частью графа?
Рассматривается раздел дискретной математики изучающий теорию графов. Приведены основные понятия теории графов такие, как вершина, ребро, ориентированный граф и так далее. Дано понятие локальной степени. Показаны способы задания графов с их демонстрацией. Отдельно рассмотрены операции над частями графа, а так же графы и бинарные отношения.
Цель: изучить различные виды конструкций графов.
Задачи:
1 Рассмотреть понятия маршрут, путь, цепь и цикл применительно к графам.
2 Рассмотреть структуру графа дерева и леса.
Пусть G – неориентированный граф.
Маршрутом в G называется такая последовательность ребер M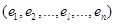 , в которой каждые два соседних ребра
, в которой каждые два соседних ребра  и
и 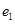 имеют общую вершину. В маршруте одно и то же ребро может встречаться несколько раз. Начало маршрута – вершина
имеют общую вершину. В маршруте одно и то же ребро может встречаться несколько раз. Начало маршрута – вершина  , инцидентная ребру
, инцидентная ребру 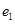 и не инцидентная
и не инцидентная 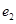 ; конец маршрута
; конец маршрута 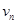 инцидентен
инцидентен 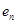 и не инцидентен
и не инцидентен  . Если
. Если  - кратные, требуется дополнительное указание, какую из двух инцидентных вершин считать началом (концом) маршрута.
- кратные, требуется дополнительное указание, какую из двух инцидентных вершин считать началом (концом) маршрута.
Маршрут, в котором совпадают его начало и конец 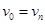 , (т.е. замкнутый), называется циклическим. Маршрут, в котором все ребра разные, называется цепью. Цепь, не пересекающая себя, т.е. не содержащая повторяющихся вершин, именуется простой цепью.
, (т.е. замкнутый), называется циклическим. Маршрут, в котором все ребра разные, называется цепью. Цепь, не пересекающая себя, т.е. не содержащая повторяющихся вершин, именуется простой цепью.
Циклический маршрут называется циклом, если он является цепью, и простым циклом, когда это – простая цепь.
Вершины 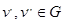 называются связанными, если существует маршрут М с началом
называются связанными, если существует маршрут М с началом  и
и 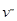 концом. Связанные маршрутом вершины связаны также и простой цепью. Отношение связанности вершин обладает свойствами эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества
концом. Связанные маршрутом вершины связаны также и простой цепью. Отношение связанности вершин обладает свойствами эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества  . Граф G называется связанным, если все его вершины связаны между собой. Поэтому все подграфы G(
. Граф G называется связанным, если все его вершины связаны между собой. Поэтому все подграфы G( ) связаны и называются связанными компонентами графа. Каждый н-граф распадается единственным образом в прямую сумму своих связанных компонент
) связаны и называются связанными компонентами графа. Каждый н-граф распадается единственным образом в прямую сумму своих связанных компонент 
Пусть G – ориентированный граф.
Последовательность ребер, в которой конец каждого предыдущего ребра  совпадает с началом следующего
совпадает с началом следующего 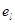 , называется путем(в нем все ребра проходят по их ориентации). В пути одно и то же ребро может встречаться несколько раз. Началом пути является начало
, называется путем(в нем все ребра проходят по их ориентации). В пути одно и то же ребро может встречаться несколько раз. Началом пути является начало  ребра
ребра 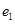 , концом пути – конец
, концом пути – конец 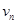 ребра
ребра 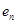 .
.
Путь называется ориентированной цепью (или просто цепью), если каждое ребро встречается в нем не более одного раза, и простой цепью, если любая вершина графа G инцидентна не более чем двум его ребрам.
Контур – путь, в котором 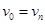 . Контур называется циклом, если он является цепью, и простым циклом, когда это – простая цепь. Если граф содержит циклы, то он содержит и простые циклы. Граф, не содержащий циклов, называется ациклическим.
. Контур называется циклом, если он является цепью, и простым циклом, когда это – простая цепь. Если граф содержит циклы, то он содержит и простые циклы. Граф, не содержащий циклов, называется ациклическим.
Вершина 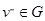 называется достижимой из вершины
называется достижимой из вершины  , если существует путь
, если существует путь 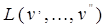 с началом
с началом  и концом
и концом 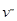 .
.
Орграф G именуется связным, если он связен без учета ориентации дуг, и сильно связен, если из любой вершины  в любую
в любую 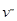 существует путь.
существует путь.
Число ребер маршрута (пути) называется его длиной.
Расстояние d( ,
,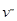 ) между вершинами
) между вершинами  и
и 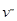 н-графа G называется минимальная длина простой цепи с началом
н-графа G называется минимальная длина простой цепи с началом  и концом
и концом 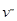 . Центромназывается вершина н-графа, от которой максимальное из расстояний до других вершин являлось бы минимальным. Максимальное расстояние от центра G до его вершины называется радиусомграфа r(G).
. Центромназывается вершина н-графа, от которой максимальное из расстояний до других вершин являлось бы минимальным. Максимальное расстояние от центра G до его вершины называется радиусомграфа r(G).
Эйлеров цикл – цикл графа, содержащий все ребра графа. Эйлеров граф– граф, имеющий эйлеров цикл (эйлеров цикл можно считать следом пера, вычеркивающего этот граф, не отрываясь от бумаги).
Теорема Эйлера: конечный неориентированный граф G эйлеров тогда и только тогда, когда он связен и степени всех его вершины четны.
Эйлерова цепь – цепь, включающая все ребра данного конечного н-графа G, но имеющая различные начало  и конец
и конец 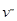 . Чтобы в конечном н-графе G существовала эйлерова цепь, необходимы и достаточны его связанность и четность степеней всех вершин, кроме начальной
. Чтобы в конечном н-графе G существовала эйлерова цепь, необходимы и достаточны его связанность и четность степеней всех вершин, кроме начальной  и конечной
и конечной 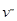 (
( и
и 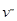 должны иметь нечетные степени). Чтобы в конечном орграфе существовал эйлеров цикл, необходимы и достаточны его связанность, а так же равенство степеней вершин этого графа по входящим и выходящим ребрам, т.е.
должны иметь нечетные степени). Чтобы в конечном орграфе существовал эйлеров цикл, необходимы и достаточны его связанность, а так же равенство степеней вершин этого графа по входящим и выходящим ребрам, т.е.  .
.
Гамильтонов цикл – простой цикл, проходящий через все вершины рассматриваемого графа. Гамильтонова цепь – простая цепь, проходящая через все вершины графа, с началом и концом в разных вершинах  .
.