Эквивалентность и порядок
Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 4.
Отношение «жить в одном городе» на множестве людей.
Пусть на множестве 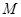 задано отношение эквивалентности
задано отношение эквивалентности 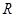 . Осуществим следующее построение. Выберем элемент
. Осуществим следующее построение. Выберем элемент 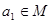 и образуем класс
и образуем класс  (подмножество
(подмножество 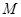 ), состоящий из элемента
), состоящий из элемента  и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент
и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс
и образуем класс  , состоящий из
, состоящий из  и эквивалентных ему элементов. Продолжая эти действия, получим систему классов
и эквивалентных ему элементов. Продолжая эти действия, получим систему классов  (возможно, бесконечную) такую, что любой элемент из множества
(возможно, бесконечную) такую, что любой элемент из множества 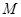 входит хотя бы в один класс, то есть
входит хотя бы в один класс, то есть  .
.
Эта система обладает следующими свойствами:
1) она образует разбиение множества 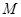 , то есть классы попарно не пересекаются;
, то есть классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов не эквивалентны.
Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы  и
и  пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен
пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен  и
и  . Тогда, в силу транзитивности отношения
. Тогда, в силу транзитивности отношения 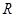 выполнялось бы
выполнялось бы  . Однако, по способу построения классов, это не возможно.
. Однако, по способу построения классов, это не возможно.
Построенное разбиение, то есть система классов – подмножеств множества 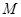 , называется системой классов эквивалентности по отношению
, называется системой классов эквивалентности по отношению 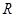 . Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества
. Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества 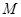 на классы само определяет некоторое отношение эквивалентности, а именно отношение «входить в один класс данного разбиения».
на классы само определяет некоторое отношение эквивалентности, а именно отношение «входить в один класс данного разбиения».
Пример 5.
Формулы, описывающие одну и ту же элементарную функцию, находятся в одном классе эквивалентности по отношению равносильности. В данном случае счётными являются само множество формул, множество классов эквивалентности (то есть индекс разбиения) и каждый класс эквивалентности.
Отношение 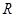 называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.
называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.
Отношение 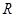 называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.
называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.
Оба типа отношений вместе называются отношениями порядка. Элементы  сравнимы по отношению порядка
сравнимы по отношению порядка 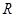 , если выполняется одно из двух отношений
, если выполняется одно из двух отношений 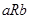 или
или 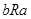 . Множество
. Множество 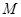 , на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным.
, на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным.