Тема 9 . Социальная политика государства
Неоклассическая модель роста Р. Солоу
Совокупный спрос в модели Солоу определяется инвестициями и потреблением (государственные закупки для простоты не учитываются): y=i+c, где i и с - инвестиции и потребление в расчете на одного занятого. Производственная функция определяет предложение на рынке товаров, а накопление капитала - спрос на произведенный продукт.
Динамика объёма выпуска зависит от объёма капитала (в нашем случае - капитала в расчете на одного занятого, или капиталовооруженности). Объём капитала меняется под воздействием инвестиций и выбытия: инвестиции увеличивают запас капитала, выбытие - уменьшает.
Инвестиции зависят от фондовооруженности и нормы накопления, что следует из условия равенства спроса и предложения в экономике: i=s-f(k). Норма накопления определяет деление продукта на инвестиции и потребление при любом значении k : y=f(k), i=sf(k), c=(l-s)-f(k).
Амортизация учитывается следующим образом: если принять, что ежегодно вследствие износа капитала выбывает его фиксированная часть d (норма выбытия), то величина выбытия будет пропорциональна объёму капитала и равна d-k. На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом d(рис.8.2.1.).
Влияние инвестиций и выбытия на динамику запасов капитала можно представить уравнением: Ak = i-dk, или, используя равенство инвестиций и сбережений, Ak - s • f(k) - dk. Запас капитала (k) будет увеличиваться (Ak>0) до уровня, при котором инвестиции будут равны величине выбытия, т.е. sf(k)=dk. После этого запас капитала на одного занятого (фондовооруженность) не будет меняться во времени, поскольку две действующие на него силы уравновесят друг друга. Уровень запаса капитала, при котором инвестиции равны выбытию (Ak=0), называется равновесным (устойчивым) уровнем фондовооруженности труда и обозначается k*. При достижении k * экономика находится в состоянии долгосрочного равновесия.
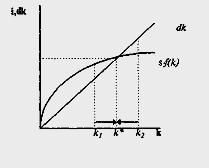
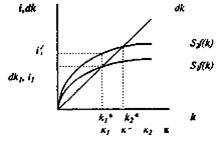
рисунок 8.2.1 рисунок 8.2.2.
Равновесие является устойчивым, поскольку независимо от исходного значения k экономика будет стремиться к равновесному состоянию, т.е. к k*. Если начальное ниже k*, то валовые инвестиции (s-f(k)) будут больше выбытия (dk) и запас капитала будет возрастать на величину чистых инвестиций. Если k2> k*, это означает, что инвестиции меньше, чем износ, а значит запас капитала будет сокращаться, приближаясь к уровню k * (см.рис. 8.2.2.).
В исходном состоянии экономика имела устойчивый запас капитала kj*, при котором инвестиции равнялись выбытию. После повышения нормы сбережения инвестиции выросли, а запас капитала (k;*) и выбытие (dkj) остались прежними. В этих условиях, инвестиции превышают превышать выбытие, что вызывает рост запаса капитала до уровня нового равновесия k2*, которое характеризуется более высокими значениями фондовооруженности и производительности труда (выпуск на одного занятого, у).( рис 8.2.3.)
Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия. Однако повышение нормы накопления ведёт к ускорению экономического роста в краткосрочном периоде, до тех пор, пока экономика не достигнет точки нового устойчивого равновесия.
Очевидно, что ни сам процесс накопления, ни увеличение нормы сбережения не могут объяснить механизм непрерывного экономического роста. Они показывают лишь переход от одного состояния равновесия к другому.
Для дальнейшего развития модели Солоу поочередно снимаются две предпосылки: неизменность численности населения и его занятой части (их динамика предполагается одинаковой) и отсутствие технического прогресса.
Предположим, население растёт с постоянным темпом п. Это новый фактор, влияющий вместе с инвестициями и выбытием на фондовооруженность. Теперь уравнение, показывающее изменение запаса капитала на одного работника будет выглядеть как : Ak=i-dk-nk или Ak=i-(d+n)k.
Учет в модели Солоу технологического прогресса видоизменяет исходную производственную функцию. Предполагается трудосберегающая форма технологического прогресса. Производственная функция будет представлена как Y = F(K,L-E), где Е - эффективность труда, а (L-Е) - численность условных единиц труда с постоянной эффективностью Е. Чем выше Е, тем больше продукции может быть произведено данным числом работников. Предлагается, что технологический проrpecc осуществляется путем роста эффективности труда Е с постоянным темпом g. Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп g=2%, то, например, 100 рабочих могут произвести столько же продукции, сколько ранее производили 102 рабочих. Если теперь численность занятых(Х) растет с темпом n, а Е растет с темпом g, то (L-Е) будет увеличиваться с темпом (n+g).
9.1. Социальная политика государства, её цели, инструменты и основные названия. Особенности её реализации в Республике Беларусь.