Условные средние. Линии регрессии.

Статистическая и корреляционная зависимости.

Коэффициент корреляции. Корреляционный момент

 

Виды зависимостей переменных величин.

Функциональной называется зависимость между двумя переменными величинами, при которой значению одной переменной величины соответствует одно определенное значение другой.

Статистической называется зависимость случайных величин, при которой каждому значению одной их них соответствует закон распределения другой, то есть изменение одной из величин влечет изменение распределения другой.

Корреляционной называется статистическая зависимость случайных величин, при которой изменение одной из величин влечет изменение среднего значения другой.

 

Условные средние. Линии регрессии.

Условным средним называется среднее арифметическое наблюдаемых значений величины Y, вычисленное при условии, что величина Х приняла конкретное фиксированное значение х.

Условным средним называется среднее арифметическое наблюдаемых значений величины Х, вычисленное при условии, что величина Y приняла конкретное фиксированное значение у.

Уравнение, связывающее наблюдаемые значения величины Х и условную среднюю величины Y, называется уравнением регрессии Y на Х:

.

Уравнение, связывающее наблюдаемые значения величины Y и условную среднюю величины Х, называется уравнением регрессии Х на Y:

.

Линии на координатной плоскости, соответствующие уравнениям регрессии называются линиями регрессии.

Корреляционные зависимости могут выражаться уравнениями регрессии различных видов: линейной, параболической, гиперболической, показательной и т.д.

 

Корреляционный момент и коэффициент корреляции.

Мерой корреляционной зависимости двух случайных величин Х и Y служит корреляционный момент (или ковариация), который вычисляется по формуле:

, (4.1)

где средние значения (здесь и в дальнейшем предполагается, что каждая пара значений (х_i,y_i) наблюдалась по одному разу):

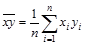, , . (4.2)

Если случайные величины Х и Y независимы, то для них m_xy=0.

Из определения корреляционного момента следует, что его размерность равна произведению размерностей изучаемых величин, Это означает, что значение корреляционного момента двух величин зависит от выбора единиц измерения этих величин. Поэтому для оценки связи величин вводится другая величина, независящая от размерности измеряемых величин и называемая коэффициентом корреляции.

Коэффициентом корреляции двух измеряемых величин Х и Y называется величина:

, (4.3)

где s_х и s_у – стандартные отклонения соответственно величин Х и Y.

Поскольку размерность корреляционного момента равна произведению размерностей величин Х и Y, а стандартные отклонения имеют размерности этих величин, то коэффициент корреляции является безразмерной величиной, и поэтому он не зависит от выбора единиц измерения изучаемых величин.

Свойства коэффициента корреляции:

1) Если две случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю, т.е. r=0.

2) Модуль коэффициента корреляции не превышает единицы, т.е. |r|£1, что эквивалентно двойному неравенству: -1£r£1.

Коэффициент корреляции, вычисленный по данным выборки, называется выборочным и обозначается r_в.

 

Вычисление в Excel корреляционных характеристик.

Ковариация (корреляционный момент) (4.1) вычисляется в Excel с помощью стандартной статистической функции КОВАР. Аргументом этой функции являются диапазоны ячеек, содержащие значения наблюдаемых величин и . Например, если значения содержатся в интервале А1:А10, а значения содержатся в интервале В1:В10, то ковариация этих величин вычисляется по формуле: =КОВАР(А1:А10; В1:В10).

Коэффициент корреляции (4.3) вычисляется в Excel одной из двух функций: КОРРЕЛ или ПИРСОН. Эти функции выдают одинаковый результат, если значения наблюдаемых величин записаны в виде чисел. Аргументы у этих функций точно такие же, как и у функции КОВАР, т.е. КОРРЕЛ(А1:А10;В1:В10) или ПИРСОН(А1:А10;В1:В10).

Иногда необходимо вычислять квадрат коэффициента корреляции, для этого имеется функция КВПИРСОН, выдающая значение r². Аргументы у этой функции такие же, как и у трех предыдущих.

 

 

§4.2. Линейная регрессия

 

Уравнением линейной регрессии (выборочным) Y на Х называется зависимость от наблюдаемых значений величины Х, выраженная линейной функцией:

, (4.4)

где величина называется выборочным коэффициентом линейной регрессии Y на Х.

Будем считать, что каждая пара значений случайных величин (х_i,y_i) наблюдалась по одному разу. В этом случае линейной зависимостью связаны сами наблюдаемые значения х_i и y_i.

Коэффициенты в уравнении линейной регрессии Y на Х (4.4) вычисляется по формулам:

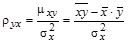и , (4.5)

где s_х – стандартное отклонение величины Х, а средние значения вычисляются по формулам (4.2).

Уравнением линейной регрессии (выборочным) Х на Y называется зависимость от наблюдаемых значений величины Х, выраженная линейной функцией:

, (4.6)

где величина называется выборочным коэффициентом линейной регрессии Х на Y.

Коэффициенты в уравнении линейной регрессии Х на Y (4.6), вычисляется по формулам:

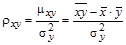и . (4.7)

где s_у – стандартное отклонение величины Y.

Если коэффициент корреляции двух величин Х и Y равен r=±1, то эти величины связаны линейной зависимостью. Коэффициент корреляции служит мерой силы (тесноты) линейной зависимости измеряемых величин. На практике, если коэффициент корреляции двух величин Х и Y |r|>0.5, то считают, что есть основания предполагать наличие линейной зависимости между этими величинами. Однако ориентироваться при выборе типа линии регрессии (линейной или нелинейной) лучше по виду эмпирической зависимости величин Х и Y.

 

Вычисление в Excel коэффициентов линейной регрессии.

Для вычисления коэффициентов линейной регрессии Y на Х (4.5) в Excel имеются следующие функции:

· НАКЛОН – вычисляет ;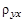

· ОТРЕЗОК – вычисляет .

Аргументами у этих функций являются диапазоны ячеек, содержащие значения и . Например, если значения находятся в интервале А1:А10, а значения находятся в интервале В1:В10, то 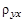вычисляется по формуле: =НАКЛОН(В1:В10; А1:А10), а вычисляется по формуле: =ОТРЕЗОК(В1:В10; А1:А10) (обязательно на первой позиции интервал значений величины Y!).

Если требуется вычислить коэффициент линейной регрессии Х на Y (4.7), то в указанных выше функциях на первую позицию следует ставить интервал значений Х, а на вторую - интервал значений переменной Y.

В Excel имеется возможность вычислить по уравнению линейной регрессии (4.4) значение переменной Y, соответствующее любому заданному значению переменной Х. Для этого существует функция ПРЕДСКАЗ(Х; диапазон_Y; диапазон_Х), где:

· Х – то значение переменной Х, для которой по формуле (4.4) следует вычислить предсказанное значение Y;

· диапазон_Y – это интервал ячеек, содержащих наблюдаемые значения ;

· диапазон_Х – это интервал ячеек, содержащих наблюдаемые значения .

Функция ПРЕДСКАЗ выдает такой же результат, который можно вычислять с помощью функций НАКЛОН и ОТРЕЗОК по формуле: =Х*НАКЛОН(диапазон_Y; диапазон_Х) + ОТРЕЗОК(диапазон_Y; диапазон_Х), где диапазон_Y и диапазон_Х – интервалы ячеек, содержащие, соответственно, значения и , а Х – адрес ячейки, содержащей значение Х (или само это число), для которого следует вычислить предсказанное Y по формуле (4.4).

 

Построение линейной регрессии с помощью Пакета анализа.

В Пакете анализа имеется инструмент анализа Регрессия, который позволяет получить коэффициенты корреляции (4.3), регрессии (4.5), их стандартные ошибки, а также характеристики, позволяющие установить, насколько хорошо полученное теоретическое уравнение линейной регрессии описывает экспериментальные данные.

Для вызова инструмента анализа Регрессия следует выполнить команду Сервис®Анализ данных®Регрессия.

Вид появившегося диалогового окна:

 

В появившемся диалоговом окне Регрессия указываются:

· в группе Входные данные в поле Входной интервал Y – адрес интервала ячеек, в которых содержатся наблюдаемые значения ;

· в поле Входной интервал Х – адрес интервала ячеек, в которых содержатся наблюдаемые значения ;

· в группе Параметры вывода активизируется переключатель Выходной интервал, и в ставшее активным поле набирается адрес ячейки, куда следует вывести результаты, а если вы хотите поместить результаты на другой рабочий лист или новый файл, то следует активизировать, соответственно, переключатели Новый рабочий лист или Новая рабочая книга;

· в группе Остатки обычно рекомендуется отметить галочкой только поле График подбора, который и будет содержать прямую регрессии;

· остальные поля можно не отмечать и нажать ОК.

В результате появится заголовок Вывод итогов и несколько таблиц и график подбора. График подбора требует дополнительного редактирования. В частности, по умолчанию линия регрессии, вычисленная по теоретическому уравнению, будет иметь вид ромбических маркеров розового цвета. Принято, чтобы прямая регрессии представляла собой сплошную линию, а точками (маркерами) отмечались только экспериментальные данные. Щелкнув по розовым маркерам точек Предсказанное Y, можно вызвать окно Формат ряда данных, и во вкладке Вид в группе Линия отметить переключатель Обычная или Другая, выбрать цвет и толщину линии, а затем в группе Маркер активизировать переключатель Отсутствует и нажать ОК.

В результате график линейной регрессии будет представлять собой требуемую прямую сплошную линию, возле которой будут располагаться экспериментальные точки.

Самая верхняя таблица итоговых вычислений называется Регрессионная статистика. В ней содержатся:

· в строке Множественный R – коэффициент корреляции r (4.3);

· в строке R-квадрат – r²;

· в оставшихся (менее важных) строках содержатся: стандартная ошибка коэффициента корреляции, число наблюдений, нормированное значение r².

Инструмент анализа Регрессия выводит большое количество результатов и мы ограничимся рассмотрением только наиболее важных и простых. Опуская описание второй итоговой таблицы Дисперсионный анализ, переходим к третьей итоговой таблице, содержащей две строки Y-пересечение и Переменная Х1:

· в первой колонке Коэффициенты и в первой строке Y-пересечение содержится коэффициент линейной регрессии ;

· во второй строке Переменная Х1 этой же колонки содержится коэффициент регрессии ;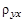

· следующая колонка Стандартная ошибка содержит стандартные ошибки коэффициентов и ;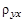

· опуская две следующие колонки, переходим к паре колонок с названиями Нижние 95% и Верхние 95%.

В этих колонках содержатся нижняя и верхняя границы доверительных интервалов (при установленной надежности 95% по умолчанию) для коэффициента (в первой строке) и коэффициента 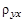(во второй строке). Эти доверительные интервалы имеют вид 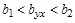и , где и 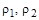- нижние и верхние границы интервалов, соответственно, для коэффициентов и 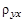. Они показывают, что с вероятностью 0,95 значения вычисленных коэффициентов и 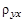могут содержаться в указанных интервалах.

Поскольку для любой выборочной характеристики необходимо, либо указывать доверительный интервал, либо оценивать их значимость, то информация, выведенная в рассматриваемой таблице, позволяет установить, насколько точно рассчитанные коэффициенты линейной регрессии описывают экспериментальную зависимость. Если доверительный интервал окажется широким, то это означает, что полученное уравнение линейной регрессии плохо описывает экспериментальную зависимость, которая, скорее всего, является нелинейной.

В последней таблице Вывод остатка содержатся вычисленные по теоретической формуле (4.4) для каждого из наблюдений предсказанные значения Y и разности между предсказанными Y и наблюдаемыми в столбце Остатки.

 

Быстрое построение линейной регрессии в Excel: линия тренда.

В Excel имеется еще более быстрый и удобный способ построить график линейной регрессии (и даже основных видов нелинейных регрессий, о чем см. далее). Это можно сделать следующим образом:

1) выделить столбцы с данными X и Y (они должны располагаться именно в таком порядке!);

2) вызвать Мастер диаграмм и выбрать в группе Тип – Точечная и сразу нажать Готово;

3) не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма, в котором следует выбрать пункт Добавить линию тренда;

4) в появившемся диалоговом окне Линия тренда во вкладке Тип выбрать Линейная;

5) во вкладке Параметры можно активизировать переключатель Показывать уравнение на диаграмме, что позволит увидеть уравнение линейной регрессии (4.4), в котором будут вычислены коэффициенты (4.5).

6) В этой же вкладке можно активизировать переключатель Поместить на диаграмму величину достоверности аппроксимации (R^2). Эта величина есть квадрат коэффициента корреляции (4.3) и она показывает, насколько хорошо рассчитанное уравнение описывает экспериментальную зависимость. Если R² близок к единице, то теоретическое уравнение регрессии хорошо описывает экспериментальную зависимость (теория хорошо согласуется с экспериментом), а если R² близок к нулю, то данное уравнение не пригодно для описания экспериментальной зависимости (теория не согласуется с экспериментом).

В результате выполнения описанных действий получится диаграмма с графиком регрессии и ее уравнением.

 

 

§4.3. Основные виды нелинейной регрессии

 

Параболическая и полиномиальная регрессии.

Параболической зависимостью величины Y от величины Х называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):

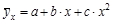. (4.8)

Это уравнение называется уравнением параболической регрессии Y на Х. Параметры а, b, с называются коэффициентами параболической регрессии. Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.

Уравнение (4.8) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной зависимостью величины Y от величины Х называется зависимость, выраженная полиномом n-ого порядка:

, (4.9)

где числа а_i (i=0,1,…, n) называются коэффициентами полиномиальной регрессии.

 

Степенная регрессия.

Степенной зависимостью величины Y от величины Х называется зависимость вида:

. (4.10)

Это уравнение называется уравнением степенной регрессии Y на Х. Параметры а и b называются коэффициентами степенной регрессии.

Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение

ln =lna+b·lnx. (4.11)

Это уравнение описывает прямую на плоскости с логарифмическими координатными осями lnx и ln . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки логарифмов эмпирических данных lnx_i и lnу_i находились ближе всего к прямой (4.11).

 

Показательная регрессия.

Показательной (или экспоненциальной) зависимостью величины Y от величины Х называется зависимость вида:

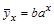(или 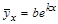). (4.12)

Это уравнение называется уравнением показательной (или экспоненциальной) регрессии Y на Х. Параметры а (или k) и b называются коэффициентами показательной (или экспоненциальной) регрессии.

Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение

ln =x·lna+lnb (или ln =k·x+lnb). (4.13)

Это уравнение описывает линейную зависимость логарифма одной величины ln от другой величины x. Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки эмпирических данных одной величины x_i и логарифмы другой величины lnу_i находились ближе всего к прямой (4.13).

 

Логарифмическая регрессия.

Логарифмической зависимостью величины Y от величины Х называется зависимость вида:

=a+b·lnx. (4.14)

Это уравнение называется уравнением логарифмической регрессии Y на Х. Параметры а и b называются коэффициентами логарифмической регрессии.

 

Гиперболическая регрессия.

Гиперболической зависимостью величины Y от величины Х называется зависимость вида:

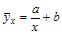. (4.15)

Это уравнение называется уравнением гиперболической регрессии Y на Х. Параметры а и b называются коэффициентами гиперболической регрессии и определяются методом наименьших квадратов. Применение этого метода приводит к формулам:

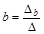, , (4.16)

где:

, , (4.17)

.

В формулах (4.16-4.17) суммирование проводится по индексу i от единицы до количества наблюдений n.

К сожалению, в Excel нет функции, вычисляющих коэффициенты гиперболической регрессии. В тех случаях, когда заведомо не известно, что измеряемые величины связаны обратной пропорциональностью, рекомендуется вместо уравнения гиперболической регрессии искать уравнение степенной регрессии, так в Excel имеется процедура ее нахождения. Если же между измеряемыми величинами предполагается гиперболическая зависимость, то коэффициенты ее регрессии придется вычислять с помощью вспомогательных расчетных таблиц и операций суммирования по формулам (4.16-4.17).

 

Быстрое построение нелинейных регрессий в Excel с помощью тренда.

В Excel с помощью добавления линии тренда можно быстро построить, помимо линейной регрессии, следующие виды нелинейных регрессий: логарифмическая, полиномиальная, степенная, экспоненциальная.

Для построения графика нелинейной регрессии, так же как при построении линейной регрессии, необходимо построить график экспериментальных точек (точечная диаграмма) и, не сбрасывая выделения с полученной диаграммы, выполнить команду Диаграмма®Добавить линию тренда. В появившемся диалоговом окне во вкладке Тип выбрать наиболее подходящий для данных экспериментальных точек тип нелинейной регрессии. Во вкладке Параметры следует отметить Показывать уравнения на диаграмме и Поместить на диаграмме величину достоверности аппроксимации (R^2) (при необходимости).

В результате будет проведена кривая линия, называемая линией тренда или регрессии, к которой ближе всего располагаются экспериментальные точки. На этой диаграмме также будут выведены уравнение соответствующей регрессии и коэффициент достоверности аппроксимации (квадрат коэффициента корреляции в случае линейной зависимости). Величина , так же как и для линейной зависимости, показывает, насколько точно полученное уравнение регрессии описывает зависимость экспериментальных данных. Если близок к единице, то полученное уравнение регрессии с достаточной степенью точности хорошо описывает экспериментальную зависимость (теория согласуется с экспериментом). Если близок к нулю, то выбранный тип нелинейной регрессии плохо описывает экспериментальную зависимость (теория не согласуется с экспериментом).

 

Практические задания