Амплитудно-частотные характеристики

Универсальной амплитудно-частотной характеристикой (АЧХ) для всех видов связи контуров является зависимость тока второго контура от частоты. Выразим её через параметры связанных контуров, используя соотношения, полученные в лекциях (15) и (17).

С учётом потерь суммарные сопротивления первого и второго контуров, рассматриваемых как последовательные, согласно формулам (15.4) и (15.8) равны

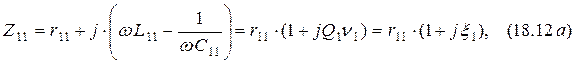
где

– обобщённая расстройка контура с соответствующим индексом.

Контурные токи (17.4) будут равны

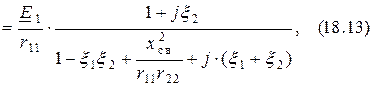
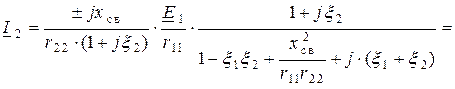
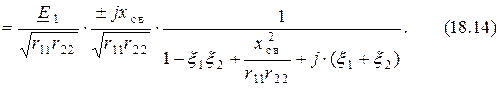
Преобразуем третье слагаемое в знаменателе формулы (18.14), используя понятие добротности контура (15.6),

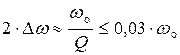Учитывая, что обычно и полоса пропускания контура (15.18) равная весьма мала, то в её пределах, учитывая приближённое равенство , можно пользоваться приближённым выражением (18.15)

Поэтому, преобразуя формулы (18.13) и (18.14), получим

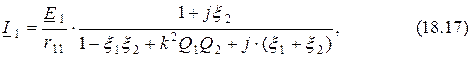
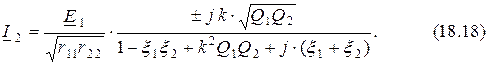
Представим АЧХ системы связанных контуров в относительных единицах как отношение модуля тока второго контура к максимальной величине этого модуля. Так как согласно формуле (17.20) , то получаем

В системе связанных контуров по технологическим причинам дешевле и проще оба контура делать одинаковыми. В этом весьма часто встречающемся слу­чае выполняются условия 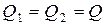, и . Поэтому

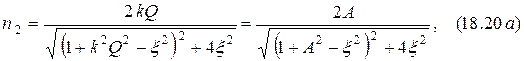
где – фактор связи.

Преобразуя подкоренное выражение

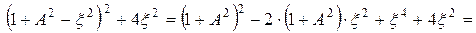
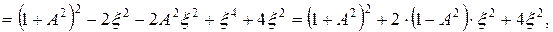
окончательно получаем формулу относительной АЧХ связанных контуров по току

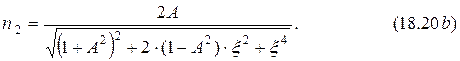
Найдём экстремумы АЧХ в зависимости от обобщённой расстройки. С этой целью возьмём первую производную и приравняем её нулю

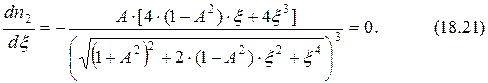
Решая, получим

Так как обобщённая расстройка не может быть мнимым числом, то 2-й и 3-й корни существуют при .

Добротности контуров являются постоянными величинами. Поэтому изменение фактора связи 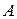может происходить только за счёт изменения коэффициента связи .

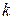Первому и единственному корню при соответствует максимум амплитудно-частотной характеристики на резонансной частоте:

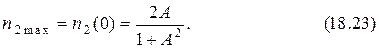
С увеличением 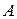от нуля до единицы максимум коэффициента передачи растёт также от нуля до единицы (рис. 18.2).

При 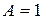все три корня совпадают. В этом случае связь между контурами и коэффициент связи называют критическими, причём

При для значений корней (18.22) имеем

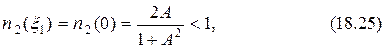
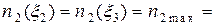
Следовательно, АЧХ системы связанных контуров при является двугорбой с минимумом на резонансной частоте (рис. 18.2).

 

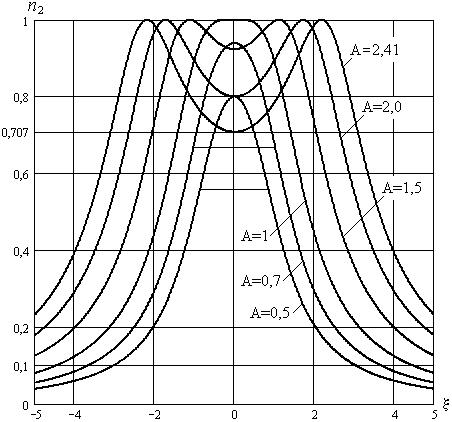
Рис. 18.2. Амплитудно-частотные характеристики системы двух связанных контуров

 

При 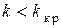связь называют слабой, при – сильной. Слабой связи соответствует одногорбая, сильной – двугорбая АЧХ.

Увеличивать фактор связи можно только до такой величины, чтобы минимум на резонансной частоте достигал стандартного уровня определения полосы пропускания, то есть уровня 0,707. При большей величине 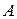провал АЧХ приводит к тому, что вместо одной появляются две полосы пропускания, расположенные по обе стороны от резонансной частоты. Это недопустимо.

Согласно формуле (18.25) получаем условие нахождения максимально допустимого значения фактора связи

Решая, получим

С учётом формулы (15.18) полоса пропускания связана с граничным значением обобщённой расстройки соотношением

где величину можно найти из формулы

которую с учётом формул и (18.23) при преобразуем к виду

Решая, находим

Анализ выражения (18.32) показывает, что при 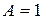полоса пропускания системы связанных контуров в 1,41 раза шире полосы пропускания одиночного контура. С уменьшением фактора связи полоса пропускания сужается и при становится равной полосе пропускания одиночного контура. При имеем и . То есть этот предельный случай практически не реализуем.

Для согласно формуле (18.26) имеет место равенство и поэтому выражение (18.31) преобразуется к виду

Решая, найдём граничное значение обобщённой расстройки

В этом случае с увеличением фактора связи полоса пропускания (18.29)

расширяется и при становится в 3,10 раза шире полосы пропускания одиночного контура.

Систему связанных контуров лучше сравнивать с двухкаскадным усилителем, в каждый каскад которого включёны одинаковые одиночные колебательные контуры. Выигрыш от использования системы связанных контуров по сравнению с двухкаскадным усилителем заключается в получении более плоской АЧХ в пределах полосы пропускания и более прямоугольной формы.

Сравним эти схемы друг с другом.

АЧХ двухкаскадного усилителя (ДУ) находится как произведение АЧХ контуров, описываемых формулой (15.11). Отсюда

Формулу для расчёта полосы пропускания на уровне можно получить, приравняв правую часть , так как :

Решая относительно , находим его зависимость от

Поэтому формулу для расчёта полосы пропускания двухкаскадного усилителя можно найти как

Коэффициентом прямоугольности называют отношение полосы пропускания на выбранном уровне к полосе на стандартном уровне . Чем меньше коэффициент прямоугольности, тем лучше избирательные свойства отдельного контура, системы связанных контуров или многокаскадного усилителя. Поэтому

Для значения находим, что .

Формулу для расчёта полосы пропускания системы связанных контуров при на выбранном уровне можно получить из выражения (18.20), приравняв его правую часть величине , где определяется формулой (18.23):

Решая уравнение относительно , находим

и полосу пропускания

Поэтому коэффициент прямоугольности при будет равен

Формулу для расчёта полосы пропускания системы связанных контуров при можно получить из выражения (18.33), приравняв правую его часть выбранной величине :

Решая относительно , находим

и формулу полосы пропускания

Коэффициент прямоугольности равен

Значения коэффициента прямоугольности в зависимости от фактора связи и выигрыш по прямоугольности системы из двух связанных контуров по сравнению с двухкаскадным усилителем приведены в табл. 18.1. Из таблицы видно, что при критической связи коэффициент прямоугольности двухкаскадного усилителя примерно в полтора раза больше, чем у системы из двух связанных контуров, а при максимально допустимой связи – в 2 раза. Следовательно, однокаскадный усилитель со связанными контурами имеет более прямоугольную АЧХ, чем двухкаскадный усилитель с одиночными контурами такой же добротности.

 

Таблица 18.1

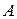
	0,1	0,3	0,5	0,7	1,0	1,5	2,0	2,41
связ. конт.	4,633	4,423	4,068	3,668	3,154	2,705	2,473	2,341
W	1,01	1,05	1,15	1,27	1,48	1,72	1,88	1,99

 

 

[1] В лекции рассматривается только трансформаторная связь, а остальные виды связи студенты изучают самостоятельно