Метод равносильных преобразований
Метод аналитических таблиц
Метод истинностных таблиц.
Методы установления общезначимости формул.
Метод истинностных таблиц.
Метод аналитических таблиц.
Метод от противного.
Метод равносильных преобразований.
Составляется истинностная таблица формулы. Если в своем последнем столбце она содержит только значения И, значит, эта формула общезначима, в противном случае – необщезначима.
Аналитические таблицы строятся по аналитическим правилам.
Введем обозначения: Т-«true»- истина; F-«false»- ложь.
Правила для логических операций(два правила для каждой операции)

| 
| 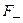
| 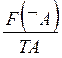
|
| TÙ | 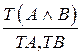
| FÙ | 
|
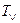
| 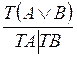
| 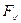
| 
|

| 
| 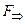
| 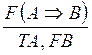
|

| 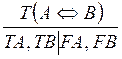
| 
| 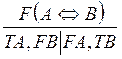
|
Пример. Установить, является ли формула
 общезначимой.
общезначимой.
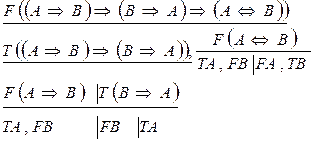
Выпишем итоговые таблицы:
1){TA,FB,TA,FB} незамкнутая;
2){TA,FB,FA,TB} замкнутая;
3){FB,TA,FB} незамкнутая;
4){TA,TA,FB} незамкнутая;
5){FA,FA,TB} замкнутая;
6){TA,FB,TB} замкнутая.
Среди итоговых таблиц есть незамкнутые, следовательно, формула не является общезначимой.
Если все итоговые таблицы формулы с индексом F-замкнуты, то формула является общезначимой.
Пример. Проверить, является ли логическим противоречием формула  ?
?

1){FA} незамкнута;
2){TB,FA,TA} замкнута. Следовательно,  - не есть логическое противоречие
- не есть логическое противоречие
Замечание:Метод аналитических таблиц используется обычно для формул, в которых число атомов больше трех-четырех (тогда не строятся таблицы истинности).
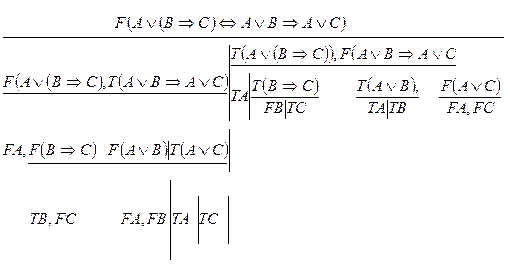 Пример.Доказать, что формула
Пример.Доказать, что формула  общезначима
общезначима
1) {FA,TB,FC,FA,FB} – замкнутая;
2) {FA,TB,FC,TA} – замкнутая;
3) {FA,TB,FC,TC} – замкнутая;
4) {TA,TA,FA,FC} – замкнутая;
5) {TA,TB,FA,FC} – замкнутая;
6) {FB,TA,FA,FC} – замкнутая;
7) {TC,TA,FA,FC} – замкнутая;
8) {FB,TB,FA,FC} – замкнутая;
9) {TC,TB,FA,FC} – замкнутая.
Все таблицы замкнутые, значит, формула является общезначимой.
Если при исследовании формул на общезначимость, итоговые таблицы этой формулы с индексом Fвсе замкнуты, то она является общезначимой. Аналогично, если формула исследуется с индексом Т и все итоговые таблицы замкнуты, то она является противоречием. В противном случае формула является нейтральной.
3.3.3 Метод от противного связан с решением логических уравнений.
Логическое уравнение - это равенство вида: Ф =Ф
=Ф ,где Ф
,где Ф и Ф
и Ф -формулы алгебры высказываний, или одно из значений «И», «Л». Решить логическое уравнение - означает найти все те наборы истинностных значений атомов, входящих в хотя бы одну из формул Ф
-формулы алгебры высказываний, или одно из значений «И», «Л». Решить логическое уравнение - означает найти все те наборы истинностных значений атомов, входящих в хотя бы одну из формул Ф и Ф
и Ф , при котором имеет равенство:
, при котором имеет равенство:
Ф =Ф
=Ф .
.
Пример: проверить, общезначима ли формула (АÞВ) Þ ((ВÞ С)Þ (АÞС)).
Предположим противное. Пусть формула не является общезначимой, т.е. существует набор атомов, на котором она принимает значение Л:
(АÞВ) Þ ((ВÞ С)Þ (АÞС))=Л.
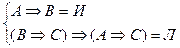
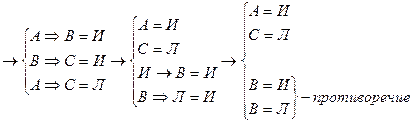
Полученное противоречие свидетельствует о том, что формула «И» во всех интерпретациях, т.е. общезначима.
Отметим, что на общезначимые эквиваленции из формул 1-50 можно смотреть как на равносильности.
Пример.Рассмотрим формулу (15)
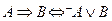 можно заменить на
можно заменить на 
Основной идеей при преобразовании формул с помощью основных равносильностей является стремление получить значение «И» на основе применения законов склеивания, идемпотентности, поглощения и формул:

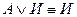
 ,
,
а также упрощения на основе формул
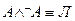
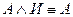


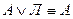
Пример.С помощью метода равносильных преобразований установить, общезначима ли формула 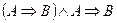 .
.
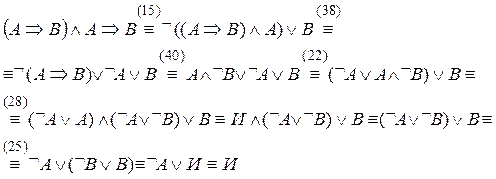
Формула общезначима