ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

 

Рассмотрим маленькую площадку dS с единичным вектором нормали (рис.23.1).

Поток вектора определяется через скалярное произведение вектора поля и элементарную площадку:

. (23.14)

Поток вектора − скалярная величина.

Таким образом, поток через элементарную площадку можно записать в виде:

dФ = EdS cos a = E_n dS.

Поток через конечную поверхность S равен:

.

Найдем поток вектора через замкнутую поверхность.

а) Рассмотрим точечный заряд. Пусть для начала имеем поверхность, окружающую заряд, в виде сферы с центром в точке нахождения заряда (рис. .

 

Так как вектор параллелен нормали, то имеем

Итак, если заряд q расположен внутри сферы, то поток равен:

.

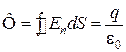Если заряд находится снаружи (рис. 23.2, б), то Ф = 0, (сколько силовых линий вошло, столько и вышло).

б) Пусть заряд q находится внутри произвольной замкнутой поверхности S (рис. 23.3). Определим поток через любой элемент этой поверхности dS

.

где dΩ = dS/r² − элемент телесного угла.

Можно показать, что поток вектора через любую поверхность S равен опять произведению заряда на полный телесный угол:

.

Независимо от вида поверхности, охватывающей заряд, и независимо от вида заряда поток вектора напряженности электростатического поля определяется зарядом, который охвачен поверхностью.