ВЗАИМОСВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

Единицей потенциала является вольт (В).

Оказывается, что зная потенциал j(r) данного электрического поля, можно достаточно просто восстановить и само поле .

Приравняв правые части формул (23.1) и (23.5), получим выражение, которое определяет связь между напряженностью и потенциалом:

. (23.7)

Приращение djв формуле(23.7)является полнымдифференциалом от координат (x, y, z), т. е.

.

Скалярное произведение в правой части (23.7) равно сумме произведений проекций вектора перемещения и напряженности поля:

.

Подставив это выражение в (23.7) и приравняв коэффициенты при dx, dy и dz, получим:

, , . (23.8)

Если подставить выражения (23.8) для проекций в формулу для вектора 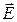, то получим соотношение:

, (23.9)

где:

называется градиентом потенциала.

Согласно принципу суперпозиции для напряженности поля можно записать, используя формулу (23.9):

. (23.10)

В формуле (23.10) j = j₁ + j₂ + … , т. е. принцип суперпозиции оказывается справедливым и для потенциала.