Амплитудная модуляция [1,25].

Амплитудная модуляция(amplitude modulation, АМ) была первым видом модуляции, освоенным на практике. В настоящее время АМ применяется в основном только для радиовещания на низких частотах (не выше коротких волн) и для передачи изображения в телевизионном вещании. Это обусловлено низким КПД использования энергии модулированных сигналов.

АМ соответствует переносу информации s(t) Þ U(t) при постоянных значениях параметров несущей частоты w и фазы j. АМ – сигнал представляет собой произведение информационной огибающей U(t) и гармонического колебания ее заполнения. Форма записи амплитудно-модулированного сигнала:

u(t) = U(t)×cos(wot+jo), (15.1.1)

U(t) = Um×[1+M×s(t)], (15.1.2)

где Um – постоянная амплитуда несущего колебания при отсутствии модулирующего сигнала s(t), М – коэффициент амплитудной модуляции.

Значение М характеризует глубину амплитудной модуляции. В простейшем случае, если модулирующий сигнал представлен одночастотным гармоническим колебанием с амплитудой So, то коэффициент модуляции равен отношению амплитуд модулирующего и несущего колебания М=So/Um. Значение М должно находиться в пределах от 0 до 1 для всех гармоник модулирующего сигнала. При значении М<1 форма огибающей несущего колебания полностью повторяет форму модулирующего сигнала s(t), что можно видеть на рис. 15.1.1. Малую глубину модуляции М<<1 для основных гармоник модулирующего сигнала применять нецелесообразно, т.к. при этом мощность передаваемого информационного сигнала будет много меньше мощности несущего колебания и мощность передатчика будет использоваться неэкономично.

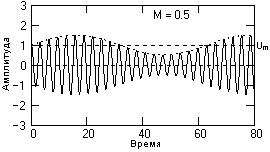
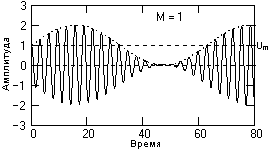
Рис. 15.1.1. Модулированный сигнал. Рис. 15.1.2. Глубокая модуляция

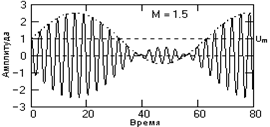Рис. 15.1.3. Перемодуляция сигнала

На рис. 15.1.2 приведен пример глубокой модуляции, при которой значение M стремится к 1. Стопроцентная модуляция (М=1) может приводить к искажениям сигналов при перегрузках передатчика, если он имеет ограниченный динамический диапазон по амплитуде несущих частот или ограниченную мощность передатчика (увеличение амплитуды несущих колебаний в пиковых интервалах сигнала U(t) в два раза требует увеличения мощности передатчика в четыре раза).

При М>1 возникает так называемая перемодуляция, пример которой приведен на рис. 15.1.3. Форма огибающей при перемодуляции искажается относительно формы модулирующего сигнала, и после демодуляции, если применяются ее простейшие методы, информация может быть искажена.

Однотональная модуляция. Простейшая форма модулированного сигнала создается при модуляции несущего сигнала гармоническим колебанием с одной частотой W:

u(t) = Um[1+M×cos Wt]×cos wot. (15.1.3)

Значения начальных фазовых углов несущего и модулирующего колебания для упрощения выражений будем принимать равными нулю, если они не имеет принципиального значения. С учетом формулы cos(x)×cos(y) = (1/2)[cos(x+y)+cos(x-y)], из выражения (15.1.3) получаем:

u(t) = Um cos wot + (UmM/2) cos[(wo+W)t] + (UmM/2) cos[(wo-W)t]. (15.1.4)

Рис. 15.1.4. Физические спектры сигналов.

Отсюда следует, что модулирующее колебание с частотой W перемещается в область частоты wo и расщепляется на два колебания, симметричные относительно частоты wo, с частотами соответственно (wo+W) - верхняя боковая частота, и (wo-W) - нижняя боковая частота (рис. 15.1.4 для сигнала, приведенного на рис. 15.1.1). Амплитуды колебаний на боковых частотах равны друг другу, и при 100%-ной модуляции равны половине амплитуды колебаний несущей частоты. Если получить уравнение (15.1.4) с учетом начальных фаз несущей и модулирующей частоты, то правило изменения фаз аналогично изменению частоты: начальная фаза модулирующего колебания для верхней боковой частоты складывается с начальной фазой несущей, для нижней – вычитаются из фазы несущей. Физическая ширина спектра модулированного сигнала в два раза больше ширины спектра сигнала модуляции.

Энергия однотонального АМ-сигнала.Обозначим раздельными индексами (нес- несущая, вб- верхняя боковая, нб- нижняя боковая) составляющие колебания в левой части выражения (15.1.4) однотональногоАМ-сигнала и определим функцию его мгновенной мощности:

u(t) = uнес(t) + uвб(t) + uнб(t).

p(t)= u2нес(t)+u2вб(t)+u2нб(t)+2uнес(t)uвб(t)+2uнес(t)uнб(t)+2uвб(t)uнб(t). (15.1.5)

Для определения средней мощности сигнала выполним усреднение функции p(t):

Pu =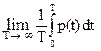

Все взаимные мощности модулированного сигнала при усреднении становятся равными нулю (спектры не перекрываются), при этом:

Pu = Рнес + Рвб + Рнб = Um2/2 + (UmM)2/4. (15.1.6)

Доля мощности боковых частот в единицах мощности несущей частоты:

(Рвб + Рнб)/Рнес = М2/2, (15.1.7)

т.е. не превышает 50% даже при 100%-ной модуляции.

Под полезной мощностью модулированных сигналов понимают мощность боковых частот, несущих информацию. Коэффициент полезного действия модуляции определяется отношением мощности боковых частот к общей мощности модулированного сигнала:

hАМ = (Um2 M2/4) /Pu = M2/(М2+2). (15.1.8)

Рис. 15.1.5.

Как можно видеть на рис. 15.1.5, даже при М=1 КПД амплитудной модуляции составляет только 33%, а при практическом использовании обычно меньше 20%.

Для модулированных сигналов применяют также понятие пиковой мощности Pmax. Значение пиковой мощности для однотонального АМ-сигнала:

Pmax = Um2 (1+M)2.

Многотональный модулирующий сигнал имеет произвольный спектральный состав. Математическая модель такого сигнала может быть аппроксимирована тригонометрической суммой гармонических составляющих, в пределе бесконечной:

s(t, n) =an cos(Wnt+Fn), (15.1.9)

где значения амплитуд an и начальных фаз Fn упорядоченной возрастающей последовательности гармоник Wn произвольны. Подставляя (15.1.9) в (15.1.2) и заменяя произведения M·an парциальными (частичными) коэффициентами модуляции Mn = M·an, получим обобщенное уравнение амплитудно-модулированного сигнала и его физического спектра:

u(t) = Um[1+Мncos(Wnt+Fn)]×cos wot. (15.1.10)

u(t)=Umcos wot+(Um/2)Mncos[(wo+Wn)t+Fn]+Mncos[(wo-Wn)t-Fn].

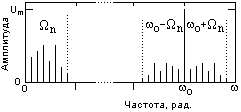Рис. 15.1.6. Многотональная модуляция.

На рис. 15.1.6 приведен схематический пример амплитудных спектров модулирующего и АМ-сигналов при многотональной модуляции. Он также содержит полосы верхних и нижних боковых частот относительно несущей частоты wo, являющихся прямой и зеркальной масштабными копиями модулирующего сигнала. Полная ширина спектра АМ-сигнала равна удвоенной ширине спектра модулирующего сигнала.

Пример.Частотный диапазон одного километра каротажного кабеля 0-200 кГц. Частотный диапазон измерительных датчиков скважинного прибора 0-5 кГц. От какого количества датчиков одновременно может передаваться информация по данному каротажному кабелю?

Минимальная несущая частота должна быть на порядок выше максимальной частоты модулирующего сигнала, т.е. порядка 50 кГц. Для передачи сигнала от одного датчика потребуется полоса частот 2×5 = 10 кГц плюс пустой защитный интервал для исключения перекрестных помех порядка 1 кГц, т.е. 11 кГц. Общее количество каналов передачи информации: (200-50-5)/11 = 13 каналов.

В соответствии огибающей модулированного сигнала форме модулирующего сообщения нетрудно убедиться вычислением модуля аналитического сигнала z(t) = u(t) + (см. тему "Аналитические сигналы").

При u(t) = Um[1+Мn·s(t, n)] cos wo(t), квадратурное дополнение сигнала определяется преобразованием Гильберта и равно = Um[1+Мn·s(t, n)] sin wo(t). Огибающая сигнала:

|z(t)| ===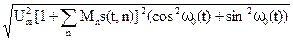 Um[1+Мn·s(t,n)].

Демодуляция АМ-сигналов может выполняться несколькими способами.

Самый простой способ – двухполупериодное детектирование (вычисление модуля сигнала) с последующим сглаживанием однополярных полупериодов несущей фильтром низких частот.

На рис. 15.1.8 приведен пример изменения однотонального амплитдно-модулированного сигнала и его физического спектра при детектировании (в реальной односторонней шкале частот и в реальной шкале амплитудных значений гармоник колебаний). Параметры представленного сигнала: несущая частота 30 Гц, частота модуляции 3 Гц, коэффициент модуляции М=1.

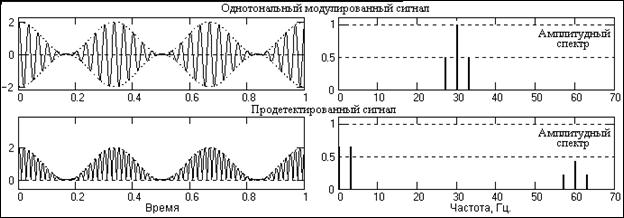
Рис. 15.1.8. Изменение однотонального модулированного сигнала при детектировании

Как видно на рисунке, при детектировании спектр модулированного сигнала становится однополярным, переходит на основную несущую частоту 2wo и уменьшается по энергии. Основная часть энергии (более 4/5) трансформируется в область низких частот и распределяется между постоянной составляющей и выделенной гармоникой сигнала модуляции в зависимости от значения коэффициента модуляции М. При М=1 энергии равны, при М=0 (в отсутствие сигнала модуляции) вся энергия переходит на постоянную составляющую.

Кроме этих составляющих в спектре появляются также 2-я, 3-я и более высокие гармоники детектированного модулированного сигнала (т.е. на частотах 4wo±W, 6wo±W, и т.д.), которые не показаны на рисунке. Энергия второй гармоники не превышает 2%, а остальных и вовсе незначительна. Демодуляторы сигнала выделяют после детектирования только низкочастотный информационный сигнал и подавляют все остальные частоты, включая постоянную составляющую (низкочастотный фильтр с подавлением постоянной составляющей).

Очевидно также, что в случае перемодуляции сигнала исходный информационный сигнал будет восстанавливаться с ошибкой.

Другой распространенный метод – синхронное детектирование. При синхронном детектировании модулированный сигнал умножается на опорное колебание с частотой несущего колебания. Без учета фазовых углов колебаний:

y(t) = u(t) cos wot = U(t) cos wot·cos wot = ½ U(t) + ½ U(t) cos 2wot. (15.1.16)

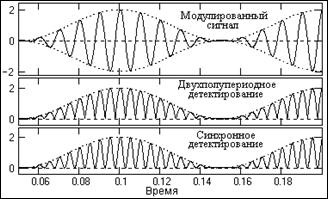Рис. 15.1.9.

Как следует из этого выражения, сигнал разделяется на два слагаемых, первое из которых повторяет исходный модулирующий сигнал, а второе повторяет модулированный сигнал на удвоенной несущей частоте 2wо.

На рис. 15.1.9 приведено визуальное сопоставление двухполупериодного и синхронного детектирования, которое наглядно показывает практически полное подобие процессов. Но форма новой несущей при синхронном детектировании является чистой гармоникой, в отличие от двухполупериодного детектирования.

Физический амплитудный спектр сигналов после демодуляции однозначно соотносится со спектром входного модулированного сигнала: амплитуды гармоник модулированного сигнала на частоте 2wо в два раза меньше амплитуд входного сигнала, постоянная составляющая равна амплитуде несущей частоты wo и не зависит от глубины модуляции, амплитуда информационного демодулированного сигнала в 2 раза меньше амплитуды исходного модулирующего сигнала.

Рис. 15.1.10.

Замечательной особенностью синхронного детектирования является полная независимость от глубины модуляции, т.е. коэффициент модуляции сигнала может быть больше 1. Пример синхронного детектирования перемодулированного сигнала приведен на рис. 15.1.10.

Однако при синхронном детектировании требуется точное совпадение фаз и частот опорного колебания демодулятора и несущей гармоники АМ-сигнала. При сдвиге фазы опорного колебания на Dw относительно несущей частоты выходной сигнал демодулятора оказывается умноженным на косинус фазовой ошибки:

y(t) = U(t) cos wot·cos(wot-Dj) = ½ U(t) cos(-Dj) + ½ U(t) cos(2wot-Dj),

и амплитуда сигнала занижается, а при Dw=p/2 становится равной нулю.

При сдвиге частоты между несущим и опорным колебаниями сигнал демодулятора оказывается умноженным на гармоническое колебание с разностной частотой:

y(t) = U(t) cos wot·cos(wot-Dw) = ½ U(t) cos(-Dwt) + ½ U(t) cos((2wo-Dw)t),

при этом выходной сигнал демодулятора начинает пульсировать с частотой биений (beat) Dw.

Для синхронизации опорного колебания с несущей частотой сигнала в составе демодуляторов используются следящие системы фазовой автоподстройки опорной частоты.

Рис. 15.1.11. Балансная модуляция.

Балансная амплитудная модуляцияили АМ с подавлением несущей частоты (АМ-ПН).Как следует из вышеприведенных данных, основная доля мощности АМ – сигнала приходится на несущую частоту. При балансной модуляции производится перемножение двух сигналов – модулирующего и несущего, при котором происходит подавление несущего колебания и КПД модуляции становится равным 100%. Так, для однотонального сигнала при U(t) = M×cos Wt имеем:

u(t) = UmM×cos Wt×cos wot = (UmM/2){cos[(wo+W)t] + cos[(wo-W)t]}, (15.1.17)

т.е. однотональный модулирующий сигнал переносится на биения двух высоких частот. Пример сигнала с балансной модуляцией приведен на рис. 15.1.11. Амплитудный спектр сигнала подобен приведенному на рис. 15.1.4 с отсутствующей несущей частотой wo. Аналогично, многотональный балансно - модулированный сигнал имеет две симметричные относительно частоты wo группы верхних и нижних боковых колебаний:

u(t) = (Um/2){Mncos[(wo+Wn)t+Fn] + Mncos[(wo+Wn)t-Fn]}. (15.1.18)

Подавление несущей частоты определяется следующим. При переходе огибающей биений U(t) через нуль фаза несущей частоты высокочастотного заполнения скачком изменяется на 1800, поскольку функция косинуса огибающей имеет разные знаки слева и справа от нуля. При этом в высокодобротной системе (с малыми потерями энергии), настроенной на частоту wo, колебания, возбужденные одним периодом биений, гасятся последующим периодом.

Однако балансная модуляция не получила широкого распространения в связи с трудностями, возникающими при демодуляции сигналов. В принципе, синхронное детектирование позволяет выполнять демодуляцию без каких-либо проблем, но при условии известной несущей частоты сигнала и точной фазовой синхронизации опорной частоты с несущей. Но во входном сигнале АМ-ПН несущая частота отсутствует. Для снятия этой трудности обычно применяют неполное подавление несущей и оставляют в модулированном сигнале определенный "остаток" несущей (пилот-сигнал), который и используется для фазочастотной автосинхронизации при демодуляции.