Волновые функции, описывающие электрон в атоме водорода.

 

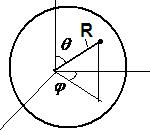
Потенциальная энергия сферически симметрична, поэтому оператор Лапласа в уравнении Шредингера обычно записывается в сферических координатах и при реше­нии (13-1в) требуется использование сферических координат, в которых ψ =ψ(r,θ,φ).

Оператор Лапласа в сферических координатах представляется в виде двух частей – радиальной и угловой.

 

Поэтому:

,

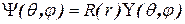где - радиальная функция, - угловая функция,

. (13-2)

Уравнение Шредингера вследствие сферической симметрии распадается на 3 уравнения, каждое из которых зависит только от одной переменной – радиальной r, меридиональной θ и азимутальной φ.

Вол­новая функция ψ должна удовлетворять 3 условиям (см. выше),а также условиюнормировки.

, (13-3)

где модуль ψ² определяет плотность вероятности найти данную частицу в объеме dV. Поэтому, уравнение (13-3) – есть условие достоверности нахождения частицы во всем пространстве.

Решение для угловой части волновой функции

А). Из условия сферической симметрии, а также условия однозначности волновой функции следует:

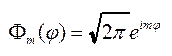
являются функциями целочисленного аргумента m который может принимать значения m=0,±1,±2…

Б). Функция Θ - непрерывная и однозначная является специальной функцией – присоединенным полиномом Лежандра. При подстановке этой функции в (13-1б) получается уравнение, которое имеет однозначные и конечные решения только при целочисленных значениях l, которые:

- могут быть отрицательными

- связаны с числом m: m=-l,…,0,…l .

В).Угловая функция Y= ΘФ зависит от l , и при решении уравнения Шредингера дает квантование момента импульса элект­рона в атоме:

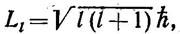(13-4)

и проекцию момента импульса на выделенное направление

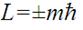. (13-5)

С точки зрения графического решения угловая функция определяет форму электронного облака и его ориентацию.

Решение для радиальной части волновой функции

Радиальная функция R выражается через шаровые функции и полиномы Лагерра. Частное решение имеет вид:

(13-6)

Где

,

А). Подстановка функции R в исходное уравнение (13-1в) дает характеристическое уравнение, из решения которого следует, что при W < 0 (элект­рон «связан» в атоме) энергия электрона определяется выраже­нием:

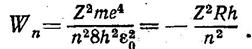(13-7)

которое описывает энергетические уровни электрона в водородоподобной системе и является аналогичным выражению в теории Бора:

Таким образом, последовательное решение уравнения Шредингера для электрона в водородоподобной системе приводит к энергетическим уровням типа Бальмера - Ридберга без использования каких-либо постулатов.

б). Найдем вероятность того, что электрон в основном состоянии атома водорода находится на расстоянии r от ядра (n=1,l=0) в интервале расстояний от r до r+dr, т. е. в шаровом слое с объемом dV=4πr²dr.Вероятность обнаружить электрон в элементе объема dV:

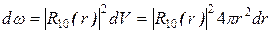
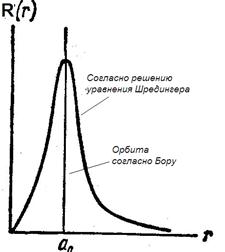
Если подставить в эту формулу выражение (13-6), то получим зависимости плотности вероятности обнаружения электрона от расстояния. Максимумы этих зависимостей дают те расстояния r_nот ядра атома, на которых электрон может быть обнаружен с наибольшей вероятностью(рис.13-1 а и б).

А)

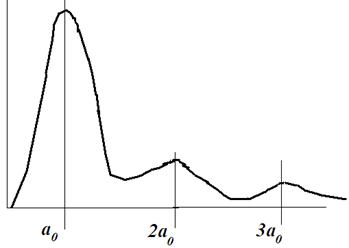Б)

Рис.13-1

 

В частности, при n=1 исследование выражения dw/dr на максимум дает r₁=а₀. Этот результат является частным случаем более общего вывода: боровские орбиты электрона представляют собой геометрические места точек, в которых электрон может быть обнаружен с наибольшей вероят­ностью.

Например, по теории Бора, вероятность обнаружить электрон в состоянии с n =1 отлична от нуля только для r₁=а₀. . Согласно же квантовой механике, эта вероятность лишь достигает максимума при r₁=а₀ , но она отлична от нуля во всем пространстве.

На рис. 13-1 со­поставлены вероятности обнаружить элект­рон на различных расстояниях от ядра по теории Бора и по квантовой механике.