Множества и действия над ними

Лекция 1. Элементы теории множеств

Литература

Язык программирования Prolog

	Язык структурированных запросов
	Стандартный язык разметки документов для Интернет
·	Объектно-ориентированный язык
	Функциональный язык программирования
·	Логический язык программирования

 

 

1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. М.:ИНФРА-М, Новосибирск, 2002.

2. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика. Харьков, «Торсинг», 2003.

3. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.:Наука, 1973.

4. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.:ФИЗМАТЛИТ, 2001.

 

Определение.Множество – это совокупность некоторых объектов, объединенных по какому-либо признаку.

Элементы, составляющие множество, обычно обозначаются малыми латинскими буквами, а само множество – большой латинской буквой. Знак ∈ используется для обозначения принадлежности элемента множеству. Запись a∈A означает, что элемент a принадлежит множеству A. Если некоторый объект x не является элементом множества A, пишут x∉A. Например, если A – это множество четных чисел, то 2∈A, а 1∉A. Множества A и B считаются равными (пишут A=B), если они состоят из одних и тех же элементов.

Если множество содержит конечное число элементов, его называют конечным; в противном случае множество называется бесконечным. Если множество A конечно, символом |A| будет обозначаться число его элементов. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ∅. Очевидно, |∅|=0.

Пример. Пусть A – множество действительных решений квадратного уравнения x²+px+q=0. Множество A конечно, |A|≤2. Если дискриминант D = p²–4q отрицателен, множество A пусто. Множество действительных решений квадратичного неравенства x²+px+q≤0 конечно, если D≤0, и бесконечно, если D>0.

Конечное множество может быть задано перечислением всех его элементов,

либо описываются их свойства. Если множество A состоит из элементов x, y, z, …, пишут A={x, y, z, …}. Например, A={0, 2, 4, 6, 8} – множество четных десятичных цифр или - множество натуральных чисел, удовлетворяющих условию х+2=1.

Введем используемое в дальнейшем понятие индексированного семейства множеств. Пусть I – некоторое множество, каждому элементу которого i сопоставлено однозначно определенное множество A_i. Элементы множества I называют индексами, а совокупность множеств A_i называют индексированным семейством множеств и обозначают через (A_i)_i∈I.

Говорят, что множество B является подмножеством множества A и пишут B⊂A, если всякий элемент множества B является элементом множества A. Например, множество натуральных чисел N является подмножеством множества целых чисел Z, а последнее в свою очередь является подмножеством множества рациональных чисел Q, то есть N⊂Z и Z⊂Q, или, короче, N⊂Z⊂Q. Легко видеть, что если B⊂A и A⊂B, то множества A и B состоят из одних и тех же элементов, и, значит, A=B, в противном случае 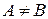. Наряду с обозначением B⊂A используется также A⊃B, имеющее тот же смысл.

Подмножества множества A, отличные от ∅ и A, называются собственными. Пустое множество и множество А называются несобственными подмножествами множества А. Совокупность всех подмножеств множества А называется его булеаном, или множеством-степенью, и обозначается через Р(А) или 2^А.

Пример. Пусть A={a, b, c}. Тогда множество 2^A состоит из следующих элементов:

{∅}, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.

Если множество A конечно и содержит n элементов, то это множество имеет 2ⁿ подмножеств, то есть |2^A |=2^|A|.

Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера-Венна. Если некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить U и изобразить его в виде всей плоскости, то любое множество 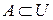можно изобразить в виде части плоскости, т.е. в виде некоторой фигуры, лежащей на плоскости.

Объединением или суммой множеств А и В называют такое множество С, которое состоит из элементов множества А, или элементов множества В, или из элеметов обоих этих множеств, т.е. . Например, если A={1,2,3} и B={2,3,4}, то A∪B={1,2,3,4}.

Пересечением или произведением двух множеств А и В называется такое множество С, которое состоит из элементов, принадлежащих одновременно обоим множествам, т.е. . Например, если A={1,2,3} и B={2,3,4}, то A∩B={2,3}.

Разностьюдвух множеств А и В называется множество, состоящее из тех и только тех элементов, которые входят в А и одновременно не входят в В, т.е.

. Например, если A={1,2,3} и B={2,3,4}, то A\B={1}.

Если, в частности, А – подмножество U, то разность U \ A обозначается и называется дополнением множества А.

Симметрической разностью (кольцевой суммой) множеств А и В называется множество , т.е. . Например, если A={1,2,3} и B={2,3,4}, то AΔB={1,4}.

 

 

 

Законы алгебры множеств:

1.Коммутативный закон: .

2.Ассоциативный закон: .

3.Дистрибутивный закон: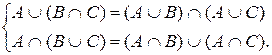

4.Законы идемпотентности: , в частности

5.Законы поглощения:

6.Законы де Моргана(двойственности):

7.Закон двойного дополнения:

8.Закон включения:

9.Закон равенства:

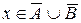Пример 1.Проверим первый из законов де Моргана. Покажем сначала, что. Предположим, что . Тогда x∉A∩B, так что x не принадлежит хотя бы одному из множеств A и B. Таким образом, x∉A или x∉B, то есть или. Это означает, что. Мы показали, что произвольный элемент множества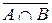является элементом множества. Следовательно, . Обратное включение доказывается аналогично. Достаточно повторить все шаги предыдущего рассуждения в обратном порядке.

Пример 2. Доказать включения

Решение.Легче всего это сделать по диаграмме Эйлера-Венна

 

 

 

Из любой пары элементов a и b (не обязательно различных) можно составить новый элемент – упорядоченную пару (a,b). Упорядоченные пары (a,b) и (c,d) считают равными и пишут (a,b)=(c,d), если a=c и b=d. В частности, (a,b)=(b,a) лишь в том случае, когда a=b. Элементы a и b называют координатами упорядоченной пары (a,b) .

Прямым (декартовым) произведением множеств A и B называется множество всех упорядоченных пар (a,b), где a∈A и b∈B. Прямое произведение множеств A и B обозначается через A×B. В соответствии с определением имеем

A×B = {(a,b)| a∈A, b∈B}. Произведение называется декартовым квадратом.

Пример 3. Даны множества А={1;2}; B={2;3}. Найти .

Решение.

.

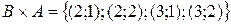Таким образом, декартово произведение не подчиняется коммутативному закону.

Пример 4.Пусть Из каких элементов состоят множества ?

Решение. Запишем множества А;В;С, перечислив их элементы:

А={3;4;5;6}; B={2;3}; C={2}. Тогда Подобно парам, можно рассматривать упорядоченные тройки, четверки и, вообще, упорядоченные наборы элементов произвольной длины. Упорядоченный набор элементов длины n обозначается через (a₁,a₂,…,a_n). Для таких наборов используется также название кортеж длины n. Допускаются в том числе и кортежи длины 1 – это просто одноэлементные множества. Кортежи (a₁,a₂,…,a_n) и (b₁,b₂,…,b_n) считаются равными, если a₁=b₁, a₂=b₂,…,a_n=b_n.

По аналогии с произведением двух множеств определим прямое произведение множеств A₁, A₂, …, A_n как множество всех кортежей (a₁,a₂,…,a_n) таких, что a₁∈A₁, a₂∈A₂, …, a_n∈A_n. Обозначается прямое произведение через A₁×A₂×…×A_n.

Понятие прямого произведения может быть обобщено на случай произвольного семейства множеств (A_i)_i∈I. Назовем I-кортежем набор элементов (A_i)_i∈I такой, что a_i∈A_i для каждого i∈I. Прямое произведение семейства множеств (A_i)_i∈I – это множество, состоящее из всех I-кортежей. Для обозначения этого множества используется символ Π_i∈IA_i и его разновидности, подобные тем, которые применяются для обозначения пересечения и объединения семейства множеств.

В случае, когда множество A умножается само на себя, произведение называют (декартовой) степенью и используют экспоненциальные обозначения. Так, в соответствии с определением A×A=A², A×A×A=A³ и т. д. Считается, что A¹=A и A⁰=∅.

Непосредственно из определений следует справедливость следующих соотношений (A∪B)×C=(A×C) ∪ (B×C);

(A∩B)×C=(A×C) ∩ (B×C);

(A\B)×C=(A×C)\(B×C).