Аксиомы теории вероятности.

Лекция №2.

Теоретической основой теории вероятности являются пять её аксиом, дополненные теоремой о вероятности суммы совместных событий.

Аксиома 1. Вероятность невозможного события равна нулю (Р(А)=0).

Аксиома 2.Вероятность достоверного события равна единице (Р(В)=1).

Аксиома 3.Вероятность случайного события заключена в пределах от нуля до единицы (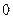<P(C)<1).

Аксиома 4.Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий (Р(А+В)=Р(А)+Р(В)). Аксиома распространяется на сумму любого конечного числа попарно несовместных событий.

Пример. В лотерее 1000 билетов: 1б. – 500 грн; 10 б. – 100 грн; 50 б. – 20 грн; 100 б. – 5 грн. Найти вероятность выиграть не менее 20 грн на приобретенный наудачу билет.

Пусть А: выиграть 500 грн. ;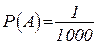

В: выиграть 100 грн.; ;

С: выиграть 20 грн.; ;

D: выиграть не менее 20 грн; ; А, В, С – несовместные события.

Формулировка следующей аксиомы 5 требует введения в рассмотрение некоторых новых понятий.

Определение. Условной вероятностьюсобытия В по отношению к событию А называется его вероятность, вычисленная в предположении, что событие А произошло. Обозначается Р(В/A).

Определение. Событие А называют независящим от события В, если вероятность появления события А не зависит от того, произошло событие В или нет (Р(А)=Р(А/B)). В противном случае А и В зависимы (P(A)P(A/B)).

Пример. Из колоды в 36 карт наудачу извлекаем одну за другой две карты. Найти вероятность того, что первая карта туз и вторая карта туз.

Существует две схемы испытания.

Схема с возвращением:

А: первая карта туз, . Карту вернули после опыта в колоду.

В: вторая карта туз, . События В и А - независимы (Р(В)=Р(В/A)).

Схема без возвращения:

А: первая карта туз; . Извлечённый туз отложен в сторону.

В: вторая карта туз, если первая тоже туз Вероятность события В зависит от того, какая карта была извлечена первой: туз или не туз. События В и А - зависимы.