СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Таблица I.

ПРИЛОЖЕНИЕ

Значения функции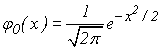

 

х		х		х		х
0.00	0.3989	1.00	0.2420	2.00	0.0540	3.00	0.0044
0.05	0.3984	1.05	0.2299	2.05	0.0488	3.05	0.0038
0.10	0.3970	1.10	0.2179	2.10	0.0440	3.10	0.0033
0.15	0.3945	1.15	0.2059	2.15	0.0396	3.15	0.0028
0.20	0.3910	1.20	0.1942	2.20	0.0355	3.20	0.0024
0.25	0.3867	1.25	0.1826	2.25	0.0317	3.25	0.0020
0.30	0.3814	1.30	0.1714	2.30	0.0283	3.30	0.0017
0.35	0.3752	1.35	0.1604	2.35	0.0252	3.35	0.0015
0.40	0.3683	1.40	0.1497	2.40	0.0224	3.40	0.0012
0.45	0.3605	1.45	0.1394	2.45	0.0198	3.45	0.0010
0.50	0.3521	1.50	0.1295	1.50	0.0175	1.50	0.0009
0.55	0.3429	1.55	0.1200	2.55	0.0154	3.55	0.0007
0.60	0.3332	1.60	0.1109	2.60	0.0136	3.60	0.0006
0.65	0.3230	1.65	0.1023	2.65	0.0119	3.65	0.0005
0.70	0.3123	1.70	0.0940	2.70	0.0104	3.70	0.0004
0.75	0.3011	1.75	0.0863	2.75	0.0091	3.75	0.0003
0.80	0.2897	1.80	0.0790	2.80	0.0079	3.80	0.0002
0.85	0.2780	1.85	0.0721	2.85	0.0069	3.85	0.0002
0.90	0.2661	1.90	0.0656	2.90	0.0060	3.90	0.0002
0.95	0.2541	1.95	0.0596	2.95	0.0051	3.95	0.0002
						4.00	0.0001

 

Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.
Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение.
В дальнейшем мы рассмотрим два типа случайных величин — дискретные и непрерывные.