Аксиомы вероятностей.

Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,

 

Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)

Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.

Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию .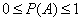

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:

P(A+B)=P(A)+P(B)

(1)

 

Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то

(2)

 

Событием, противоположным событию , называется событие , состоящее в ненаступлении события . Очевидно, события и несовместны.

Пусть, например, событие состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие заключается в том, что изделие стандарту не удовлетворяет. Пусть событие — выпадение четного числа очков при однократном бросании игральной кости; тогда — выпадение нечетного числа очков.

Теорема 1. Для любого события вероятность противоположного события выражается равенством

(3)

Теорема 2. Вероятность невозможного события равна нулю.

Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.