Свойства проводниковых материалов и зависимость их от состава и внешних факторов.

К основным свойствам проводниковых материалов относятся:

• Удельная проводимость или обратная ей величина – удельное сопротивление;
• Температурный коэффициент удельного сопротивления;
• Удельная теплопроводность;
• Контактная разность потенциалов и термоэлектродвижущая сила;
• Предел прочности при растяжении и относительное удлинение при разрыве.

 

Удельное сопротивление проводников. Величину, обратную удельной проводимости g называют удельным сопротивлением r и для проводника с постоянным поперечным сечением определяют по формуле:

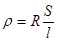(4.3)

Единицей удельного сопротивления в СИ является Ом×м, однако в практике чаще пользуются внесистемной единицей мкОм×м.

Следует отметить, что в отличие от диэлектриков диапазон удельных сопротивлений металлических проводников достаточно мал – от 0,016мкОм×м. для серебра и примерно до 10 мкОм×м. для железо-хромо-кобальто-алюминиевых сплавов, т.е. занимает всего три порядка.

 

Температурная зависимость удельного сопротивления металлических проводников. Как было показано ранее в идеально чистых металлах единственной причиной, которая ограничивает длину свободного пробега, являются тепловые колебания узлов кристаллической решетки (фононы). Удельное сопротивление металла, обусловленное этим фактором, обозначим как ρ_Т.. С ростом температуры возрастают амплитуды фононов и связанные с этим флюктуации периодического поля решетки. Это повышает рассеивание электронов, уменьшает длину свободного пробега и вызывает возрастание удельного сопротивления. Для упрощенной одномерной модели решетки длина свободного пробега электронов определяется как:

(4.4)

 

где λ_св - длина свободного пробега;

Δa - амплитуда фононов;

N - концентрация атомов в металле.

Потенциальная энергия атома, отклоненного на Δa от узла решетки:

 

W_n = ½ · K_упр (Δa)² (4.5)

 

где К_упр - коэффициент упругости связи.

Согласно классической статистике средняя энергия одномерного гармоничного осциллятора равняется КТ. Тогда:

 

½ · K_упр (Δa)² = КТ (4.6)

где К - постоянная Больцмана.

Тогда из (4.5), (4.6) получим:

 

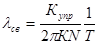
(4.7)

 

Если подставить (4.7) в (4.2) получим:

 

 

(4.8)

 

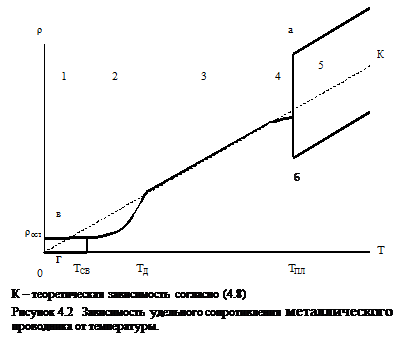То есть с ростом температуры удельное сопротивление чистых металлов должно возрастать линейно. В действительности эта зависимость является более сложной (рисунок 4.2)

На участке 3 при комнатных температурах зависимость ρ = ¦(Т) линейна, как это видно из (4.8). То есть с ростом температуры возрастает амплитуда тепловых колебаний узлов кристаллической решетки, что уменьшает длину свободного пробега электронов.

На участке 4 вблизи температуры плавления имеет некоторая нелинейность, что объясняется другими механизмами рассеивания электронов.

При переходе металла из твердого состояния в жидкое (температура плавления Т_пл) может иметь место как резкое возрастание удельного сопротивления (а), так и его уменьшение (б). Это связано с изменением структуры кристаллической решетки. Если при плавлении объем металла возрастает, что имеет место для большинства металлов, то расстояние между атомами тоже возрастает, металлическая связь уменьшается, а амплитуда фононов возрастает, что уменьшает длину свободного пробега электронов, следовательно, сопротивление металла возрастает. Для некоторых металлов (висмут, галлий) при плавлении объем металла уменьшается, что усиливает связи между атомами, амплитуда фононов уменьшается и удельное сопротивление тоже уменьшается.

На участке 5 металлы находятся в жидком состоянии и сохраняют кристаллическую решетку, поэтому зависимость удельного сопротивления от температуры поясняется аналогично участку 3.

На участке 2, ниже температуры Дебая (Т_Д) изменяется частота тепловых колебаний узлов кристаллической решетки, поэтому зависимость ρ = ¦(Т) нелинейна и подчиняется закону:

ρ = A·Tⁿ (4.9)

где n - изменяется от 1 до 5.

На участке 1 некоторые металлы имеют конечное сопротивление (r_ост) даже при температуре Т=0 К. Это объясняется наличием в металле статических дефектов решетки, прежде всего примесей. Это позволяет оценивать чистоту металлов на основании отношения:

ρ_300K / ρ_4K

 

где ρ_300K , ρ_4K - соответственно удельное сопротивление металла при 300 К и 4,2 К (температура кипения жидкого гелия). Чем меньше это отношение, тем чище металл.

У некоторых металлов при температуре ниже Т_св наблюдается резкое уменьшение удельного сопротивления до нуля. Такое явление называют сверхпроводимостью.

Таким образом, согласно (4.9) металлические проводники в обычных условиях имеют линейную зависимость удельного сопротивления от температуры.

 

Влияние примесей на удельное сопротивление металлических проводников.Как уже говорилось, причинами рассеяния электронов в металлах являются не только тепловые колебания узлов кристаллической решетки, но и наличие статических дефектов, которые, прежде всего связанные с примесями. Рассеивание на статических дефектах не зависит от температуры. Поэтому при абсолютном нуле сопротивление реальных металлов остается конечным. Из этого следует правило Маттиссена об аддитивности удельного сопротивления:

ρ_пр = ρ_т + ρ_ост (4.10)

где ρ_пр - полное сопротивление металла с примесью;

ρ_т - сопротивление, обусловленное рассеянием электронов на фононах;

ρ_ост - остаточное сопротивление, обусловленное рассеиванием электронов на статических дефектах решетки.

Наибольший вклад в остаточное сопротивление вносит рассеяние на примесных атомах, которые практически всегда имеются в металлах. Поэтому длина свободного пробега электронов в металлах с примесью состоит из:

 

1/l_св = 1/λ_Т +1/λ_д (4.11)

где l_Т, l_Д - длина свободного пробега электронов, ограниченная фононами и примесями, соответственно.

Длина пробега l_Д:

 

1/λ_д ≈ N_d S_d (4.12)

 

где N_d - концентрация атомов примеси;

S_d – эффективная плоскость рассеивания электронов атомами примеси.

Тогда удельное сопротивление проводника с примесью:

 

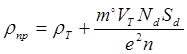(4.13)

 

 

То есть наличие примесь увеличивает удельное сопротивление металла, но его зависимости от температуры остается линейной (рис. 4.3)

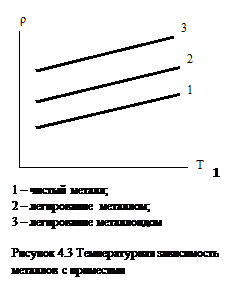Различные примеси по-разному влияют на сопротивление металла. Это зависит от деформаций кристаллической решетки атомами примеси. Чем большая разность в размерах собственных и примесных атомов, тем больше остаточное сопротивление. То есть выполнится правило Линде:

 

Dρ_ост = а +b(DZ)² (4.14)

 

где Dρ_ост - изменение остаточного сопротивления при изменении примеси;

DZ - разность валентностей собственного атома и атома примеси;

а, b - константы.

Таким образом, на сопротивление металлов меньшее влияние оказывают примесные атомы металла, а большее – атомы металлоидов.

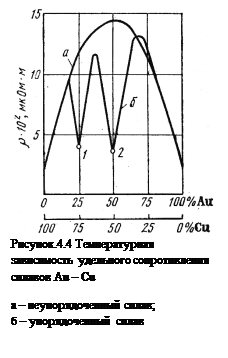В технике очень широко используют металлические сплавы, имеющие значительную концентрацию атомов примеси, со структурой неупорядоченного твердого раствора. Статическое распределение атомов разного вида в узлах кристаллической решетки вызывает значительные флюктуации периодического поля кристалла, рассеивающего электроны. Но в неупорядоченных твердых растворах, преимущественно с добавкой примеси, изменяется только период решетки. Поэтому действителен закон Нордгейма:

Dρ_ocт = C^.x_A^.x_B = C^. x_B (1-x_B) = C^.x_A(1-x_A) (4.15)

 

де С - константа;

x_А, x_В - атомные доли компонентов в сплаве.

То есть в бинарных твердых растворах А-В остаточное сопротивление возрастает, как при добавлении атомов металла В к металлу А, так и при добавленные атомов металла А к металлу В (рис. 4.4). Остаточное сопротивление достигает максимума при x_А = x_В = 0,5.

Закон Нордгейма описывает изменение остаточного сопротивления для непрерывных неупорядоченных твердых растворов. Если сплав отжечь, то он может стать упорядоченным и, если при этом возникают интерметаллические соединения, которые имеют собственную кристаллическую решетку, то зависимость остаточного сопротивления разделяется на части, соответственно числу интерметаллических соединений. Таким образом, удельное сопротивление металлических сплавов всегда выше сопротивления чистых металлов. Это свойство используется для получения высокоомных проводниковых материалов.

Изменение удельного сопротивления при упругих деформациях объясняется изменением амплитуды колебания узлов кристаллической решетки металла. Увеличение амплитуды колебания узлов решетки металла приводит к уменьшению длины свободного пробега носителей заряда и удельное сопротивление возрастает. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может вновь снижено до первоначальных значений.

 

Температурный коэффициент удельного сопротивления.В диа­пазоне температуры, где зависимость r от t близка к линейной (рис. 4.2, участок 3) допустима линейно-кусочная аппроксимация этой зависимости, и величина удельного сопротивления в конце диапазона температу­ры t может быть подсчитана по формуле

r_t = r₀(1+a_rt) (4.16)

где r₀—удельное сопротивление в начале диапазона.

Величину a_r из выражения (4.) называют средним темпера­турным коэффициентом удельного сопротивления в данном диа­пазоне температуры:

 

, К^-1 (4.17)

 

Дифференциальное выражение для a_r имеет вид

 

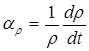, К^-1 (4.18)

Значения a_r чистых металлов в твердом состоянии близки друг к другу, и поэтому приближенно можно считать a_r » 0,004 , К^-1.

Исключение составляют элементы, относящиеся к ферромагнетикам — железо, никель, кобальт, гадолиний, а также натрий, ка­лий, хром и др., однако и для них a_r отличается от приведенной величины только в 1,5—2 раза.

Наличие примесей уменьшает значение α_ρ. У некоторых сплавов α_ρ. даже может приобретать небольшие отрицательные значения (рис.4.5). Это объясняют тем, что при более сложных составе и структурax по сравнению с чистыми металлами сплавы нельзя рассматривать как класси­ческие металлы, т. е. изменение проводи­мости их обусловливается не только из­менением подвижности носителей заряда но в некоторых случаях и частичным возрастанием концентрации носителей при повышении температуры. Сплав, у кото­рого уменьшение подвижности с увеличе­нием температуры компенсируется воз­растанием концентрации носителей заря­да, имеет нулевой температурный коэф­фициент удельного сопротивления.

Это явление используется для изготовления термостабильных сплавов, например, константана, манганина ). Константан - сплав с 60% Ni и 40% Сu имеет большое сопротивление (~0,5 мкОм×м) и очень малый температурный коэффициент (меньше 10^-6 К^-1), отсюда и его название.

 

Удельная теплопроводность металлов. Высокая теплопроводность металлов легко объясняется посредством передачи тепловой энергии атомов нагретого участка металла атомам холодного участка за счет переноса этой энергии коллективизированными электронами. Так как механизм электропроводности и теплопроводности в металлах обусловлен одними и теми же факторами: движением электронного газа и его плотностью, очевидно, что металлы с высокой электропроводностью являются также хорошими проводниками тепла, а диэлектрики обладают не только низкой электропроводностью, но и низкой теплопроводностью. Так, медь имеет удельную теплопроводность 406 Вт/К×м, серебро 453 Вт/К×м, алюминий 218 Вт/К×м, что значительно выше чем у диэлектриков. Удельная теплопроводность и электропроводность металлов связаны законом Видемана-Франца:

 

l_Т / σ = L₀Т (4.19)

где l_Т - удельная теплопроводность.

σ - удельная электропроводность.

L₀ - число Лоренца.

Поскольку на участке комнатных температур удельная электропроводность падает пропорционально температуре, то согласно (4.19), удельная теплопроводность металлов не должна зависеть от температуры. Это следствие из закона Видемана-Франца выполняется для большинства металлов. Это свойство применяют в технике, при использовании металлов как радиаторов для охлаждения мощных полупроводниковых приборов.

Для этой цели необходимо использовать металлы с большим значением удельной теплопроводности. Чаще всего, это сплавы на основе алюминия (силумин), которые имеют хорошие тепловые, механические и антикоррозийные свойства. Медь нельзя использовать вследствие её плохой коррозионной стойкости, а серебро - вследствие высокой стоимости.

Контактные явления и термоэлектродвижущая сила (термо-э.д.с.)

При соприкосновении двух разных металлов, между ними возникает контактная разность потенциалов. Согласно квантовой теории причиной этого является различная энергия Ферми соприкасающихся металлов. Пусть в изолированном состоянии электронный газ в металлах А и В имеет энергию Ферми W_F^A и W_F^B, отсчитываемую от дна зоны проводимости (рис.4.6).

Термодинамическая работа выхода электронов из металла равняется, соответственно, c_А и c_В. Поскольку кинетическая энергия электронов, которые находятся на уровне Ферми в разных металлах различна, то при контакте материалов возникает значительный переход электронов из металла В с большим значением энергии Ферми в металл, где эта энергия меньше. Например, из металла В в металл А. Вследствие этого металл В заряжается положительно, а металл А - отрицательно. Между ними возникает разность потенциалов, которая блокирует дальнейший переход носителей заряда. Равновесие наступит, если:

 

eU_K = W_F^B - W_F^A (4.20)

 

где U_K - контактная разность потенциалов.

 

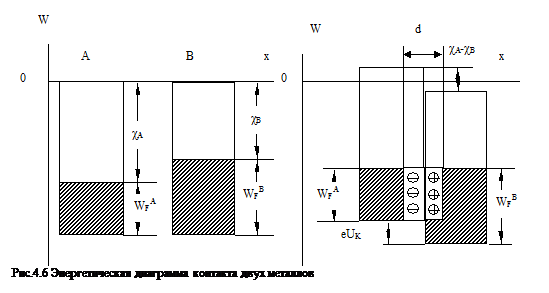
Наличие контактного поля обеспечивает равновесие потоков электронов из одного металла в другой. Равновесие вследствие большой скорости теплового движения устанавливается очень быстро (приблизительно за 10^-16 с). Двойной слой d, который возникает при этом в области контакта, будет очень тонким (приблизительно равным периоду решетки), поэтому он не влияет на прохождение электрического тока через контакт. Поскольку энергия Ферми в металлах значительна, то контактная разность потенциалов достигает несколько вольт.

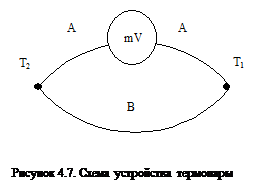
Термоэлемент, который построен из двух различных металлических проводников с замкнутой цепью, называют термопарой (рис.4.7).

Вольтметр в такой цепи будет показывать разность потенциалов, которую называют термоэлектродвижущей силой (термо-э.д.с.). Термо-э.д.с. равняется:

U @ a_T (Т₂ - Т₁) (4.21)

где a_T — относительная удельная термо-э.д.с.

Значение a_T зависит от природы материалов и температуры и включает в себя три составляющих. Первая обусловлена температурной зависимостью контактной разности потенциалов, поскольку с ростом температуры уровень Ферми в металлах незначительно, но смещается.

Вторая составляющая обусловлена диффузией носителей заряда от горячих спаев к холодным. Поскольку существует градиент температуры от контакта к контакту, то возникает диффузия электронов от горячего контакта к холодному, что дает некоторый вклад в возникающую разность потенциалов.

Третья составляющая возникает вследствие захвата электронов квантами тепловой энергии. Их поток тоже передвигается к холодному контакту. Значение a_T приблизительно равняется нескольким мкВ/К.

Термопары часто используют для измерения температуры. Если температуру холодного контакта поддерживать 0 ^ОС, то вольтметр будет показывать напряжение пропорциональное температуре горячего контакта. Достоинством термопар является высокая линейность, возможность измерения температуры в широком интервале температур, независимость значения термо-э.д.с. от длины проводников.

Вследствие того, что значение a_T зависит от состава материала и незначительно от температуры, термопары градуируют, используя точки плавления металлов: свинца, олова, серебра и других.

Наиболее распространенными термопарами являются:

· Хромель- копель (типа ХК). Она позволяет измерять температуры до 600 ^ОС и имеет при этой температуре термо-э.д.с. приблизительно 50 мВ.

· Хромель-алюмель (типа ХА). Она используется к температурам 1000 ^ОС и имеет при этой температуре термо-э.д.с. приблизительно 40 мВ.

· Медь-константан. Ее используют при низких температурах до 350 ^ОС. При этой температуре термо-э.д.с. достигает 15 мВ.

· Платинородий-платина (типа ПП или ППР). Ее применяют до температуры 71600 ^ОС. Термо-э.д.с. у этой термопары невелика (приблизительно 14 мВ при 1600 ^ОС). Но она позволяет обеспечить наиболее точные и стабильные измерения температуры.

 

Однако явление термо-э.д.с. имеет и отрицательные стороны. В реальных условиях исключить градиенты температур практически невозможно. Поэтому, если контактируют различные металлы, то возможно возникновение паразитной термо-э.д.с. Для устранения этого в цепях (прежде всего электроизмерительных устройств), надо подбирать контактирующие металлы с малыми значениями термо-э.д.с. Такой парой, например, является медь-манганин.