Виды проводников
Основные сведения о проводниковых материалах
Проводниковые материалы
К проводниковым материалам относятся вещества, основным свойством которых является электропроводность. Проводниками электрического тока могут служить твердые тела, жидкости, а при соответствующих условиях и газы. Газы и пары, в том числе и пары металлов, при низких напряженностях электрического поля не являются проводниками. Однако если напряженность поля выше некоторого критического значения, обеспечивающего начало ударной и фотоионизации, то газ может стать проводником, обладающим электронной и ионной электропроводностями. Все проводниковые материалы подразделяются на проводники первого и второго рода.
Твердые проводники являются важнейшими проводниковыми материалами, широко применяемыми в радиоэлектронике и электротехнике. К ним относят металлы и их сплавы. По характеру применения в радиоэлектронной технике металлические материалы разделяют на металлы высокой проводимости и сплавы высокого сопротивления.
Особенности поведения электронов в металлах.
В классической электронной теории металлов были введены представления об электронном газе, состоящем из коллективизированных (свободных) электронов, концентрация которых принималась равной числу атомов в единице объема металла. К электронному газу применялись понятия и законы статистики обычных газов. Гипотеза об электронном газе была подтверждена рядом опытов. Однако не все вопросы удалось решить с точки зрения классической электронной теории металлов, так как возникли некоторые противоречия с опытными данными. Они заключались в расхождении кривых зависимости удельного сопротивления от температуры, наблюдаемой на опыте и теоретической, несоответствии теоретически получаемых значений теплоемкости металлов опытным данным.
Эти противоречия удалось объяснить с помощью квантовой волновой механики. В соответствии с этой теорией электроны в металлах следует рассматривать при обычных температурах как «вырожденный» газ. В этом состоянии энергия газа практически не зависит от изменения температуры. Тепловое движение почти не изменяет энергию электронов, а тепловая энергия расходуется на тепловые колебания узлов кристаллической решетки. Вследствие этого средняя тепловая скорость электронов не изменяется при изменении температуры. Средняя скорость направленного движения электронов под действием электрического поля зависит от вероятности столкновения электронов с узлами кристаллической решетки, что приводит к уменьшению их средней скорости.
В электронном газе, который находится в состоянии вырождения, скорости хаотического движения электронов определяются не температурой тела, а концентрацией свободных электронов. В металлах она достигает около 1028м3 , что обусловлено особенностью металлической связи, т.е. практически все валентные электроны в металлах свободны. Однако энергии эти электронов различны.
Все уровни с энергией меньше уровня Ферми с вероятностью большей 0,5 заполнены электронами, и наоборот уровни с энергией большей уровня Ферми с вероятностью 0,5 свободны от электронов. Распределение электронов по уровням энергии можно представить рисунком 4.1.
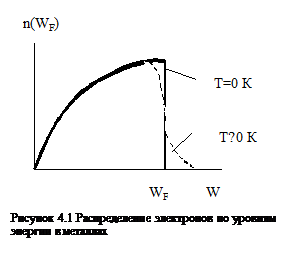Для того чтобы описывать движение электрона в твердом теле, как свободное перемещение заряженной частицы без учета периодического поля кристаллической решетки вводится понятие об эффективной массе m°, которая может быть и больше и меньше массы свободного электрона и даже иметь положительный или отрицательный знак. Металлы с преобладанием положительных эффективных масс носителей заряда (например, алюминий) называют электронными, противоположные (например, цинк, молибден) – дырочными. Первые характеризуются отрицательными знаками коэффициента Холла и термо-э.д.с. Однако, для ряда металлов, например меди, серебра, золота, коэффициент Холла имеет отрицательный знак, а термо-э.д.с. положительный, что говорит о большой сложности их электронного строения и неприменимости к ним простейших моделей.
Поведение электронов в металлах описывается статистикой Ферми-Дирака. При температуре 0 К концентрация электронов равняется:
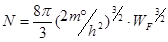(4.1)
где h - постоянная Планка;
WF - энергия уровня Ферми;
m° - эффективная масса
Вследствие того, что электронный газ находится в состоянии вырождения, в процессе электропроводности принимают участие не все свободные электроны, а только те, энергия которых больше энергии Ферми. Под влиянием электрического поля проходит рассеивание электронов под большими углами в процессе их упругих столкновений с узлами кристаллической решетки. Вследствие этого возрастает избыток быстрых электронов, которые двигаются против направления поля, и дефицит быстрых электронов с противоположным направлением скорости. Концентрация свободных электронов в чистых металлах отличается незначительно и практически не зависит от температуры, поскольку в вырожденном электронном газе энергия Ферми изменяется незначительно. Согласно квантовой теории электропроводность металлов s равняется:
σ = e2 n λвол/(m° ×VT) = (e2 n2/3 λвол /h )·(8π/3)1/3 ( 4.2)
где VT - тепловая скорость электронов;
е – заряд электрона;
п – количество электронов
λвол - длина свободного пробега электронов, которая зависит от температуры.
То есть, как видно из (4.2) электропроводность металлов не должна зависеть от температуры. Однако такая зависимость существует. Это можно объяснить волновым характером движения электронов.
Из физики известно, что электроны имеют свойство корпускулярно-волнового дуализма. То есть движение электронов можно рассматривать как перемещение плоских волн. В периодическом потенциальном поле, которое имеет идеальная кристаллическая решетка, такая волна должна перемещаться без потерь (без затухания). Это означает, что длина пробега электронов должна быть бесконечной, тогда согласно (4.2) и электропроводность металлов тоже должна быть бесконечной. Но в реальной действительности в кристаллах всегда имеют место дефекты решетки: динамические - тепловые колебания узлов кристаллической решетки, и статические - одномерные, линейные дефекты решетки.
Эти дефекты сыграют роль центров рассеивания, которые ограничивают длину свободного пробега электронов, и вследствие этого металлы имеют конечное удельное сопротивление. Таким образом, удельное сопротивление металлических проводников зависит в первую очередь от средней длины свободного пробега электронов.