Практическое занятие 1.2. Операции над множествами.
Вопросы и задания для подготовки к занятию:
1. Дайте определения понятиям «объединение множеств», «пересечение множеств». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
2. Сформулируйте свойства операций объединение и пересечение множеств. Проиллюстрируйте их с помощью кругов Эйлера.
3. Дайте определения понятиям «разность множеств», «дополнение множества». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
4. Сформулируйте свойства разности множеств.
5. Известно, что 
. Следует ли из этого, что:
° 
° 
° 
6. Найдите пересечение, объединение, разность
° [1; 5] и [3; 7];
° А=
;
° 
;
° 
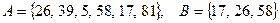и
;
° ; 
Ø..
7. Известно, что 
. Следует ли из этого, что:
° 
° 
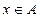
8. Найдите разность числового отрезка [1; 5] и числового отрезка [3; 7].
9. Сформулируйте условия, при которых истинны следующие высказывания:
° 
;
° 
.
Задания для самостоятельной работы
1. Перечислите элементы, принадлежащие пересечению множества букв в слове «математика» и множества букв в слове «грамматика». Из каких элементов состоит объединение данных множеств?
2. Р – множество натуральных делителей числа 18, Н – множество натуральны делителей числа 24. укажите характеристическое свойство элементов пересечения множеств Р и Н и перечислите его элементы.
3. Найдите пересечение и объединение множеств К и М, если К – множество двузначных чисел, М – множество нечетных чисел. Верно ли, что: а) 21
; б)
; в) 
; г) 
.
4. 
Найти объединение и пересечение множеств А и В, если 
и 
.
5. Три множества Р, Н, М изображены тремя прямоугольниками (рис. 1). Отметьте штриховкой области, изображающие множество Х: а) М
Н; б) Р
Н; в) (РН) 
(НМ).
Рис. 1.
6. В – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит объединение и пересечение множеств В и Т. Нарисуйте по две фигуры из каждого множества.
7. Даны множества: А ={а, b, с, d, е}, В ={с, d, f, k}, С = {b, с, d, f, m}. Перечислите элементы множеств К=(АÈВ)ÇС и Р =А È ВÇ С. Содержится ли элемент m в множестве К, а элемент f в множестве Р?
8. А – множество чисел, кратных 2, В – множество чисел, кратных 3, С – множество чисел, кратных 5. Укажите характеристическое свойство элементов множества (АВ) С и (АВ) С.
9. Найдите объединение и пересечение множеств и дайте графическую иллюстрацию при помощи диаграмм Эйлера - Венна, если:
а) А = {5, 6, 7, 8, 9, 10}, В = {8, 9, 10, 11};
б) А= {х ÷ х = 5п, п ÎN}, В= {х ÷ х = 2п, п ÎN};
г) А={х ÷ х = 2п, п ÎN}, В= {х ÷ х = 2п, п ÎN}.
10. Изобразите на числовой прямой и запишите при помощи неравенства объединение и пересечение множеств Р и Q:
а) Р = 
, Q=
;
б) Р = 
, Q = 
;
в) Р =
, Q = 
11. Множество А состоит из натуральных чисел от 2 до 10, множество В – из натуральных чисел от 5 до20. Перечислите элементы множеств А \ В и В \ А.
12. Р – множество двузначных чисел, М – множество четных натуральных чисел. изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и М и укажите характеристическое свойство элементов, принадлежащей этой разности. Верно ли, что Р \ М содержит числа 21; 17?
13. Дано множество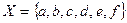 
. Запишите два подмножества множества Х и дополнение этих подмножеств до множества Х.
14. Сформулируйте характеристическое свойство элементов дополнения множества Р до множества треугольников, если: а) Р – множество остроугольных треугольников; б) Р – множество равносторонних треугольников.
15. Найдите дополнение множества У до множества Х, если:
a) Х – множество точек прямой АВ;
b) множество точек отрезка АВ;
c) Х – множество точек квадрата, У – множество точек круга, вписанного в этот квадрат.
16. Найдите дополнение:
d) множества четных натуральных чисел до множества N;
e) множества отрицательных чисел до множества Z;
f) множества целых чисел до множества Q.
2. Отметьте на координатной прямой множество А и укажите характеристическое свойство элементов его дополнения до множества R, если: а) 
; б) 
; в)
.
3. Множества А, В и С таковы, что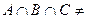 
Ø. Изобразите их при помощи кругов Эйлера и отметьте штриховкой области, представляющие множества (А \ В) С, А \ ВС, А(В \ С), АВ \ С. Для каждого случая сделайте отдельный чертеж.
4. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. постройте круги Эйлера для данных множеств и отметьте штриховкой области, изображающие множества: а) АВС; б) 
ВС; в) (АВ)'С.
5. Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите штриховкой области, представляющие множества:
а) АÈВ\С, б) А\СÈВ\С; в) А\(ВÈС).
Практическое занятие 1.3. Разбиение множества на классы. Декартово произведение множеств.
Вопросы и задания для подготовки к занятию:
1. Дайте определение понятиям «разбиение множества на классы»; «декартово произведение множеств».
2. Какими свойствами обладает и не обладает операция «декартово произведения множеств»?
3. Найдите В ´ С и С ´ В если
a. В = {1, 2, 3} C = {10, 20, 30};
b. В = {а, о, и} C = {м, т, к};
c. В = {красивая, добрая, вежливая} C = {Маша, Наташа};
d. В = {0, 00, 000} C = {1, 11, 111};
4. Для каждого из множеств, приведенных в предыдущем задании, составьте таблицу, в ячейках которой будут расположены элементы соответствующего декартова произведения.
5. Элементы какого декартова произведения множеств задания 3 могут быть отмечены в декартовой системе координат? Выполните соответствующие построения.
6. Из множества Р = {1, 2, 3, 4, 5, 6, 7, 8, 9} выделили подмножества А, В и С. В каком случае произошло разбиение множества Р на классы:
a. А ={1, 3, 5}, В = {2, 4, 6, 8}, С = {7, 9};
b. А = {5}, В = {3, 4, 8, 9}, С = {1, 6};
c. А = {1, 3, 5}, В = {2, 4, 6, 8}, С = {5, 7, 9};
d. А = {1, 3}, В = {4, 6, 8}, С = {5, 6, 9}.
7. Запишите все двузначные числа, цифры десятков которых принадлежат множеству А ={4, 5, 6}, а цифры единиц – множеству В={3, 7}.
Задания для самостоятельной работы
1. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество Е – подмножество. Состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и Е?
2. Проверьте, выполняются ли условия классификации, если: а) множество углов разбили на острые, тупые и прямые; б) множество звуков русского языка – на гласные и согласные.
3. Из множества Т треугольников выделили два подмножества: Х - подмножество прямоугольных треугольников и У – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?
4. Изобразите при помощи кругов Эйлера множество натуральных чисел и его подмножества: четных чисел и чисел, кратных 7. Можно ли утверждать, что множество N разбито:
a. на два класса: четных чисел и чисел, кратных 7;
b. на 4 класса: четных чисел, кратных 7; нечетных чисел, некратных 7; четных чисел, некратных 7; нечетных чисел, кратных 7?
5. Изобразите на координатной плоскости элементы декартова произведения множеств Х и У, если:
a. 
и 
;
b. 
и ;
c. 
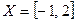и У=R;
d. Х=R и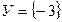 
.
6. Фигуры, приведенные на рисунке, являются результатом изображения накоординатной плоскости декартова произведения множеств Х и У. Укажите для каждой фигуры эти множества.
7. 
8. 
9.
10.
11.
12.
7. На координатной плоскости постройте прямую, проходящую через точку Р (-2, 3) и параллельную оси ОХ. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.
8. Найдите декартовы произведения множеств и изобразите их элементы на координатной плоскости:
a. А = {х÷ хÎ R, х > 0}; В = {у÷ у Î R, у < 0}
b. А = {х÷ хÎ R, х = 2}; В={у÷ у Î R , у > 0}
c. А = {х÷ хÎ R, -1 < х < 1}; В={у÷ у Î R, 0 < у < 1}.