СЛАУ с несколькими правыми частями.

При решении практических задач часто приходится решать несколько систем уравнений с одной и той же матрицей, но с разными правыми частями:

 

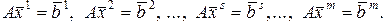(2.2.10)

 

Совокупность таких систем с общей матрицей и разными правыми

частями называется СЛАУ с m-правыми частями. Обозначим 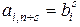и составим расширенную матрицу

 

 

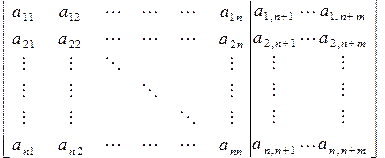
Для получения решения осуществляется общий прямой ход и обратный по каждой правой части.

 

 

2.2.5. Вычисление обратной матрицы .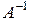

По определению обратной матрицы имеем:

,

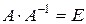где 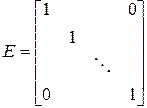– единичная матрица.

 

Следовательно, определение элементов обратной матрицы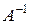

 

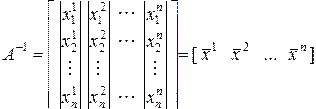(2.2.11)

 

сводится к решению 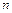систем вида

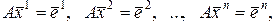(2.2.12)

где

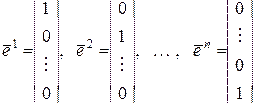– единичные векторы. (2.2.13)

 

Матрицы этих систем одинаковы. Поэтому вычисление элементов обратной матрицы сводится к решению системы с n правыми частями со следующей расширенной матрицей:

 

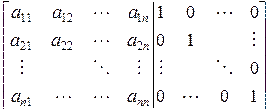. (2.2.14)