Метод Гаусса.

Общая схемарешения методом Гаусса состоит из двух частей.

1-я часть – приведение к эквивалентной системе уравнений более простой структуры (треугольной) за счет вычитания уравнений друг из друга, при умножении вычитаемого уравнения на специально подобранное число (Прямой ход).

2-я часть – решение эквивалентной системы уравнений с треугольной матрицей (Обратный ход).

 

Прямой ход (приведение системы уравнений к треугольному виду).

 

1-й шаг. Из i-ой строки (i=2, 3, ... , n) вычитаем 1-ую, умноженную на величину

,

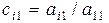получим новые коэффициенты по формуле

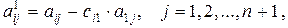
для всех .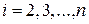

 

2-й шаг. Из i-ой строки (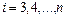) вычитаем 2-ую, умноженную на величину

,

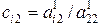получим новые коэффициенты по формуле

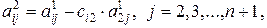
для всех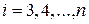

 

…………………………

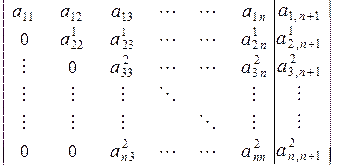
k-й шаг.Из i-ой строки (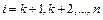) вычитаем k-ую, умноженную на величину

,

получим новые коэффициенты по формуле

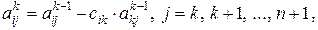
для всех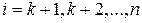

 

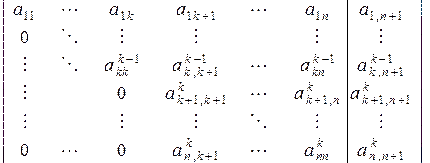
Продолжая, после 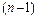шагов получим расширенную матрицу вида:

,

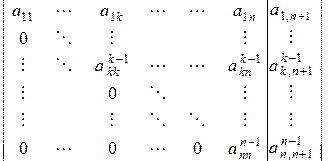т.е. систему с треугольной матрицей, эквивалентную исходной (2.2.1)-(2.2.5).

 

Общие формулы прямого хода:

(2.2.6)

Следует отметить, что элемент 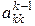– называется ведущим элементом или главным элементом.

 

Обратный ход(решение системы с треугольной матрицей).

В результате прямого хода получена следующая система с треугольной матрицей, эквивалентная исходной системе (2.2.1):

 

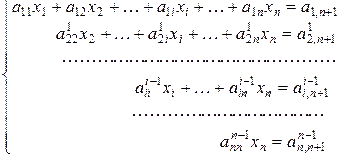(2.2.7)

 

Из треугольной системы последовательно (в обратном порядке) вычисляются значения неизвестных по формуле:

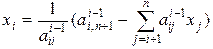(2.2.8)

для 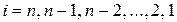(при сумма в формуле отсутствует).