Матрицы и операции над ними. Некоторые виды матриц.

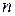Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество строк и некоторое количество столбцов (матрица размером )

. (2.1.11)

Числа и 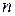называются порядками матрицы. В случае матрица называется квадратной, а число – ее порядком.

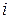Числа , входящие в состав данной матрицы называются ее элементами. В записи первый индекс обозначает номер строки, а второй индекс – номер столбца.

В случае квадратной матрицы

(2.1.12)

вводятся понятия главной и побочной диагоналей. Главной диагональю матрицы (2.1.12) называется диагональ , идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называется диагональ , идущая из левого нижнего угла в правый верхний угол.

Матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.

Для матриц определены следующие основные операции:

1. Сложение матриц по правилу

. (2.1.13)

2. Умножение матрицы на число по правилу

. (2.1.14)

Из формулы (2.1.13) непосредственно вытекает, что операция сложения матриц обладает переместительным свойством () и сочетательным свойством ().

В свою очередь, из формулы (2.1.14) ясно, что умножение матрицы на число обладает сочетательным свойством относительно числового множителя (), распределительным свойством относительно суммы матриц () и распределительным свойством относительно суммы чисел ().

Разность матрицопределяется аналогично сумме (2.1.13).

Перемножение матриц. Умножение матрицы размером на матрицу размером производится по правилу:

, (2.1.15)

где , ; .

Из сформулированного определения видно, что число столбцов матрицы было равно число строк матрицы .

Из формулы (2.1.15) вытекают следующие свойства произведения матриц: сочетательное свойство () и распределительное относительно суммы матриц свойство (или .

Произведение двух квадратных матриц одинакового порядка не обладает, вообще говоря, перестановочным свойством, т.е. в общем случае

.

Умножение матрицы на векторопределено как частный случай умножения матрицы размером на матрицу размером . Тогда,

если , то , . (2.1.16)

Диагональной матрицейназывается квадратная матрица, у которой все элементы, расположенные вне главной диагонали равны нулю, т.е.

или , (2.1.17)

Можно проверить, что произведение

равносильно умножению каждой i-ой строки матрицы на число , т.е.

.

Аналогично, произведение

равносильно умножению каждого j-го столбца на число , т.е.

.

 

 

Единичной матрицейназывается квадратная матрица, у которой все элементы, расположенные вне главной диагонали равны нулю, а все элементы, расположенные на главной диагонали равны единице, т.е.

. (2.1.18)

Элементы единичной матрицы n-го порядка определяются формулой

; . (2.1.19)

В линейной алгебре часто используется величина, называемая символом Кронекера, которую определяют как

(2.1.20)

откуда . (2.1.21)

Нулевой матрицейназывается матрица, у которой все элементы равны нулю, т.е.

. (2.1.22)

Имеют место очевидные формулы:

; . (2.1.23)

Скалярной матрицей называется диагональная матрица, у которой все элементы, расположенные на главной диагонали равны между собой.

Транспонированиемлюбой матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования матрицы получается матрица, называемая транспонированной по отношению к матрицеи обозначаемая . Элементы этой матрицы определяются формулой

.

Можно проверить, что

. (2.1.24)

Транспонированная вещественная матрица часто называется сопряженнойк матрице и обозначается .

Пусть – квадратная матрица n-го порядка, а – единичная квадратная матрица того же порядка.

Обратной матрицейпо отношению к матрице A называется матрица, обозначаемая и удовлетворяющая соотношению

. (2.1.25)

Невырожденной матрицейназывается матрица для которой существует обратная матрица . В противном случае называется вырожденной матрицей.

Некоторые свойства обратной матрицы играют важную роль в матричных вычислениях.

Обратная к произведению матрица является произведением обратных к сомножителям, взятых в обратном порядке:

. (2.1.26)

Транспонирование обратной матрицы – это то же самое, что обращение транспонированной:

. (2.1.27)

Симметричной (симметрической) матрицейназывается квадратная вещественная матрица , если для нее выполняется равенство

. (2.1.28)

Элементы матрицы в таком случае обладают свойством .

Произведение двух симметричных матриц не всегда есть матрица симметричная.

Ортогональной матрицей называется квадратная вещественная матрица , для которой выполняется равенство

, т.е. . (2.1.29)

Ортогональные матрицы обладают следующими свойствами.

1) Единичная матрица ортогональна.

2) Если матрица ортогональна, то матрица тоже ортогональна.

3) Произведение двух ортогональных матриц есть ортогональная матрица.