Линейное пространство. Евклидово пространство.

Основные понятия линейной алгебры

ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

Лекция-1

Большинство прикладных вычислительных задач, в частности задач расчета строительных конструкций и сооружений, каком-либо этапе сводится к решению задач линейной алгебры. В этом параграфе изложены основные начальные понятия из этой области.

 

Линейным пространством называется множество элементов любой природы, если выполнены следующие три требования:

I. Имеется правило, посредством которого любым двум элементам и множества ставится в соответствие третий элемент этого множества, называемый суммой элементов и и обозначаемый символом .

II. Имеется правило, посредством которого любому элементу множества и любому вещественному числу ставится в соответствие элемент этого множества, называемый произведением элемента на число и обозначаемый символом .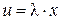

III. Указанные два правила подчинены следующим восьми аксиомам:

1) (переместительное свойство суммы);

2) 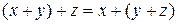(сочетательное свойство суммы);

3) существует нулевой элемент такой, что для любого элемента (особая роль нулевого элемента);

4) для каждого элемента существует противоположный элемент такой, что ;

5) для любого элемента (особая роль числового множителя );

6) (сочетательное относительно числового множителя свойство);

7) (распределительное относительно суммы числовых множителей свойство);

8) (распределительное относительно суммы элементов свойство).

Элементы произвольного линейного пространства принято называть векторами.

В сформулированном определении линейного пространства числа , , … брались из множества вещественных чисел. Поэтому определенное таким образом пространство естественно называть вещественным линейным пространством. При более широком подходе можно брать , , … из множества комплексных чисел. В результате будем иметь понятие комплексного линейного пространства.

Евклидовым пространством (вещественным евклидовым пространством)называется вещественное линейное пространство , если выполнены следующие два требования:

I. Имеется правило, посредством которого любым двум элементам этого пространства и ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом .

II. Указанное правило подчинено следующим четырем аксиомам:

1) (переместительное свойство или симметрия);

2) (распределительное свойство);

3) для любого вещественного ;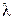

4) 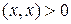, если ненулевой элемент; , если нулевой элемент.